Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Difícil)
O retângulo [tex]ABCD[/tex] abaixo representa uma mesa de bilhar.
Uma bola é lançada do ponto [tex]P[/tex], atinge o lado [tex]AB [/tex] em [tex]Q[/tex] e, em seguida, acerta o lado [tex]BC[/tex] em [tex]R,[/tex] definindo ângulos de [tex]20^\circ[/tex], conforme mostra a figura. Finalmente a bola acerta o lado [tex]AD[/tex] em [tex]S.[/tex]
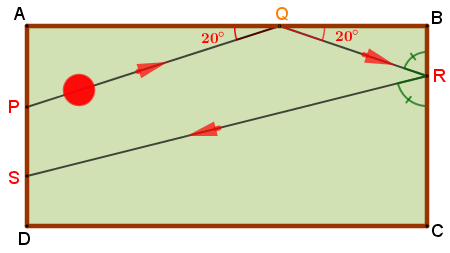
Figura não proporcional aos dados do problema.
a) Calcule a medida dos ângulos congruentes [tex]Q \hat{R}B[/tex] e [tex]C \hat{R}S.[/tex]
b) Calcule as medidas dos ângulos [tex]P \hat{Q}R[/tex] e [tex]Q \hat{R}S .[/tex]
c) O que podemos afirmar sobre as retas [tex]PQ[/tex] e [tex]RS[/tex]?

Lembretes
(1) A soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex].
(2) A soma das medidas dos ângulos internos de um polígono convexo de [tex]n[/tex] lados ([tex]n\gt 2[/tex]) é dada por:
[tex]\qquad \qquad \boxed{S_{i_n}=\left(n-2\right)\cdot 180^\circ}.[/tex]
(3) A congruência de um par de ângulos correspondentes definidos em duas retas intersectadas por uma transversal garante que essas duas retas são paralelas.
Solução
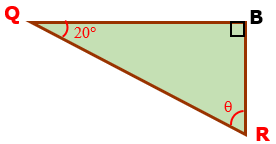
a) Observando o triângulo retângulo [tex]QRB[/tex] obtemos a medida do ângulo [tex]Q \hat{R}B[/tex] e consequentemente a do ângulo [tex]C \hat{R}S.[/tex]
Como a soma das medidas dos ângulos internos de um triângulo é [tex]180^\circ[/tex], se [tex]\theta[/tex] é a medida em graus do ângulo [tex]B\hat{R}Q[/tex], segue que:
[tex]\qquad 20^\circ+90^\circ+\theta=180^\circ[/tex]
[tex]\qquad \theta=180^\circ-20^\circ-90^\circ=70^\circ.[/tex]
Portanto, a medida dos ângulos [tex]Q \hat{R}B[/tex] e [tex]C \hat{R}S[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$70^\circ$} \, .[/tex]
b) Os pontos [tex]A[/tex], [tex]Q[/tex] e [tex]B[/tex] são colineares; logo, o ângulo [tex]A\hat{Q}B[/tex] é o que chamamos ângulo raso, ou seja, um ângulo cuja medida é [tex]180^\circ.[/tex] Da mesma forma, a medida do ângulo [tex]B\hat{R}C[/tex] é [tex]180^\circ.[/tex]
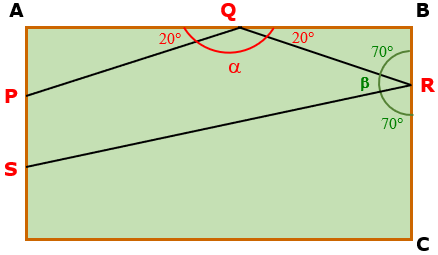
Figura não proporcional aos dados do problema.
Assim, se [tex]\alpha[/tex] e [tex]\beta[/tex] forem as medidas em graus dos ângulos [tex]P\hat{Q}R[/tex] e [tex]Q\hat{R}S[/tex], respectivamente, então:
|
[tex]\qquad 20^\circ+\alpha+20^\circ=180^\circ[/tex] [tex]\qquad \alpha=180^\circ-40^\circ[/tex] [tex]\qquad \alpha=140^\circ.[/tex] |
[tex]\qquad 70^\circ+\beta+70^\circ=180^\circ[/tex] [tex]\qquad \beta=180^\circ-140^\circ[/tex] [tex]\qquad \beta=40^\circ.[/tex] |
Logo, as medidas dos ângulos [tex]P \hat{Q}R[/tex] e [tex]Q \hat{R}S [/tex] são, respectivamente, [tex] \, \fcolorbox{black}{#eee0e5}{$140^\circ$} \, [/tex] e [tex] \, \fcolorbox{black}{#eee0e5}{$40^\circ$} \, .[/tex]
c) Observe que a medida do ângulo [tex]A\hat{P}Q[/tex] é também [tex]70^\circ[/tex]. Assim, como os ângulos [tex]A\hat{P}Q[/tex] e [tex]S\hat{P}Q[/tex] são suplementares, segue que a medida de [tex]S\hat{P}Q[/tex] é [tex]180^\circ-70^\circ=\boxed{\textcolor{#FF00FF}{110^\circ}}.[/tex]
Pelo Lembrete (2), a soma dos ângulos internos do quadrilátero convexo [tex]PQRS[/tex] é
[tex]\qquad S_{i_4}=\left(4-2\right)\cdot 180^\circ=360^\circ[/tex].
Assim, a medida do ângulo [tex]P\hat{S}R[/tex] é
[tex]\qquad 360^\circ-110^\circ-140^\circ-40^\circ= \, \boxed{\textcolor{#3BB9FF}{70^\circ}} \, .[/tex]
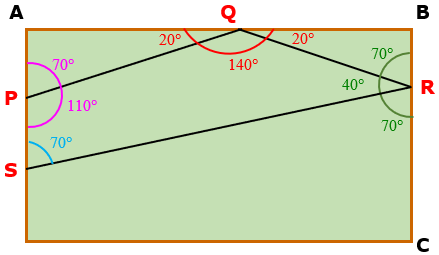
Figura não proporcional aos dados do problema.
Finalmente, observe que os ângulos [tex]A\hat{P}Q[/tex] e [tex]P\hat{S}R[/tex] são ângulos correspondentes congruentes definidos pela reta transversal [tex]AD[/tex] a partir das retas [tex]PQ[/tex] e [tex]RS[/tex]. Dessa forma, pelo Lembrete (3), as retas [tex]PQ[/tex] e [tex]RS[/tex] são paralelas.
Com isso, o traçado correto dessas duas retas é o mostrado na figura abaixo.
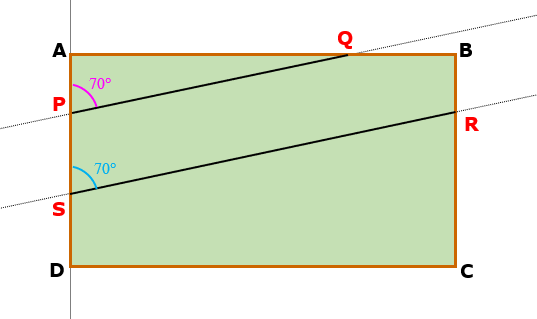
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
