Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
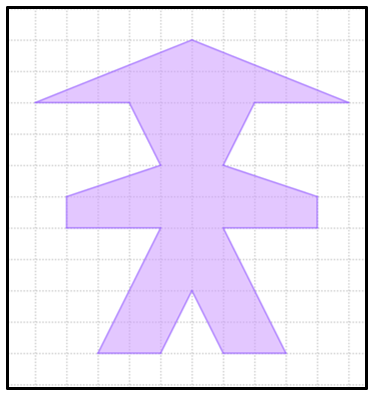
Uma decoradora vai decorar o quarto da filha de uma cliente e preparou o esboço mostrado na figura abaixo para apresentar à mãe e à filha.
O desenho será feito em uma das paredes do quarto e os lados de cada quadradinho do papel quadriculado do esboço correspondem a um comprimento real de [tex]10 \, \text{cm}[/tex].
Sabendo-se que para pintar o desenho na parede a decoradora fará duas demãos de um tipo especial de tinta, cujo litro permite pintar [tex]8\,m^2[/tex], que quantidade de tinta será necessária para a decoração proposta?
Solução
Para determinarmos a quantidade de tinta que será necessária para a decoração proposta, precisaremos calcular a medida da área que será pintada e, para isso, vamos dividir o desenho em regiões cujas áreas sabemos calcular.
Existem várias maneiras de fazermos essa divisão; uma que nos parece natural é a mostrada na figura a seguir, na qual estamos supondo que os vértices de cada polígono destacado é vértice de um quadradinho da malha quadriculada.
Vale lembrar que os lados dos quadradinhos correspondem a um comprimento real de [tex]10 \, \text{cm}[/tex].
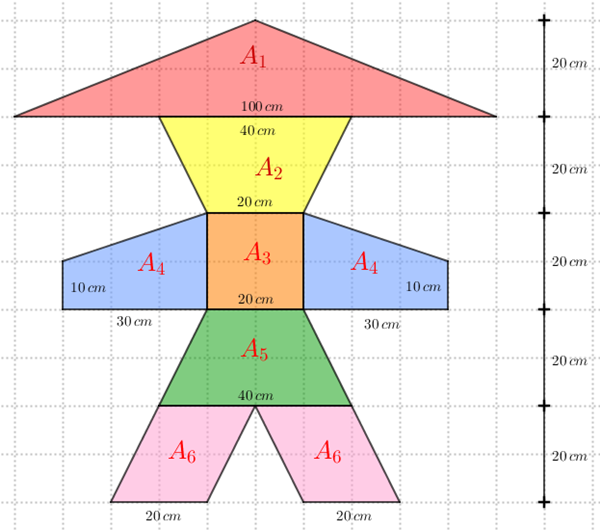
Vamos aos cálculos.
- [tex]A_1[/tex] é a área de um triângulo com [tex]100 \, \text{cm}[/tex] de base e [tex]20 \, \text{cm}[/tex] de altura. Portanto, [tex]A_1=\dfrac{100 \times 20}{2} [/tex], ou seja, [tex]\boxed{A_1=1\,000\,\text{cm}^2}. [/tex]
- [tex]A_2[/tex] é a área de um trapézio com bases medindo [tex]20 \, \text{cm}[/tex] e [tex]40 \, \text{cm}[/tex] e com altura de [tex]20 \, \text{cm}[/tex]. Com isso, [tex]A_2=\dfrac{(40 + 20) \times 20}{2} [/tex], ou seja, [tex]\boxed{A_2=600\,\text{cm}^2}. [/tex]
- [tex]A_3[/tex] é a área de um quadrado com [tex]20 \, \text{cm}[/tex] de lado. Logo, [tex]A_3=20 \times 20 [/tex], ou seja, [tex]\boxed{A_3=400\,\text{cm}^2}. [/tex]
- [tex]A_4[/tex] é a área de um trapézio com bases medindo [tex]20 \, \text{cm}[/tex] e [tex]10 \, \text{cm}[/tex] e com altura de [tex]30 \, \text{cm}[/tex]. Assim, [tex]A_4=\dfrac{(20 + 10) \times 30}{2} [/tex], ou seja, [tex]\boxed{A_4=450\,\text{cm}^2}. [/tex]
- [tex]A_5[/tex] é a área de um terceiro trapézio. Esse com bases medindo [tex]20 \, \text{cm}[/tex] e [tex]40 \, \text{cm}[/tex] e com altura de [tex]20 \, \text{cm}[/tex]. Neste caso, [tex]A_5=\dfrac{(20 + 40) \times 20}{2} [/tex], ou seja, [tex]\boxed{A_5=600\,\text{cm}^2}. [/tex]
- Por último, [tex]A_6[/tex] é a área de um paralelogramo com [tex]20 \, \text{cm}[/tex] de base e [tex]20 \, \text{cm}[/tex] de altura. Então, [tex]A_6=20 \times 20 [/tex], ou seja, [tex]\boxed{A_6=400\,\text{cm}^2}. [/tex]
Dessa forma, segue que a área [tex]A [/tex] a ser pintada pode ser assim calculada:
[tex]\qquad A=A_1+ A_ 2+ A_ 3+2\times A_ 4+ A_ 5+2 \times A_ 6[/tex]
[tex]\qquad A=1\,000+ 600+ 400+2\times 450+ 600+2 \times 400[/tex]
[tex]\qquad \boxed{A=4\,300\,\text{cm}^2} \, .[/tex]
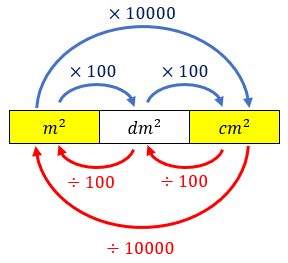
O esqueminha de conversão ao lado permite concluir que [tex]A=0,43\, m^2[/tex]; mas como serão aplicadas duas demãos de tinta, isso equivale a pintar uma área total de [tex]A_t=0,86\, m^2[/tex].
Para calcular a quantidade de tinta necessária, a partir da informação de que [tex]1[/tex] litro de tinta permite pintar [tex]8\,m^2[/tex], utilizaremos uma regrinha de três simples.
[tex] \begin{array}{c c c}
1 \, litro &\text{————–}&8 \, \text{m}^2\\
q \, litros &\text{————–}& 0,86 \, \text{m}^2
\end{array}[/tex]
Assim,
[tex]\qquad 1 \times 0,86=8 \times q \\
\qquad q=\dfrac{0,86}{8}=0,1075[/tex]
e, dessa forma, vemos que serão utilizados [tex] \fcolorbox{black}{#eee0e5}{$0,1075 \, l=107,5\,\text{ml}$}[/tex] de tinta para as duas demãos na decoração proposta.
Lembre-se de que [tex]\boxed{1 \, l=1000 \, \text{ml}}.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
