Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
(ONEM 2007) Um triângulo retângulo tem catetos com comprimentos [tex]20[/tex] e [tex]21[/tex] centímetros.
Traçaremos uma semicircunferência com centro sobre o cateto de comprimento [tex]20 \, cm[/tex] de tal forma que ela tangencie os outros dois lados do triângulo.
Qual será o raio dessa semicircunferência?

Lembretes
(1) Caso de Semelhança A.A. (ângulo – ângulo): Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes.
(2) Em triângulos semelhantes, os lados correspondentes são proporcionais.
(Há uma Sala de Ajuda sobre triângulos semelhantes no nosso Blog!)
(3) Uma reta tangente a uma circunferência é perpendicular ao raio no seu ponto de tangência.
(4) Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]A[/tex] e [tex]B[/tex], por [tex]\overline{AB}[/tex] e o seu comprimento por [tex]AB.[/tex]
Solução
Precisamos fazer uma figura com os dados do problema e para isso vamos utilizar o Teorema de Pitágoras para obtermos a medida [tex]h[/tex] da hipotenusa [tex]\overline{AC}[/tex] do triângulo [tex]ABC[/tex], que é um triângulo retângulo, cujo ângulo reto tem vértice em [tex]B:[/tex]
[tex]\qquad h^2=20^2+21^2\\
\qquad h^2=20^2+21^2\\
\qquad h=29\,cm.[/tex]
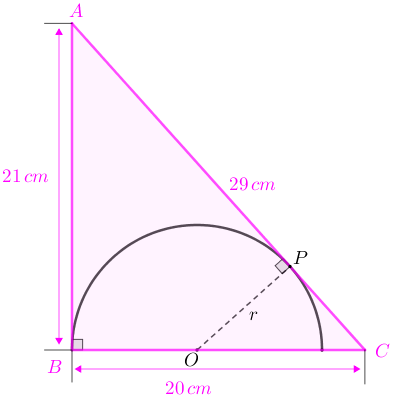
Na figura, estamos considerando que [tex]O[/tex] é o centro da semicircunferência e [tex]r[/tex] é a medida do seu raio e que os pontos de tangência dos lados do triângulo a essa semicircunferência são [tex]P[/tex] e [tex]B.[/tex]
Observe, agora, que o ângulo de vértice [tex]\hat C[/tex] é comum aos triângulos retângulos [tex]ABC[/tex] e [tex]OPC[/tex]; assim, devido às medidas de seus ângulos internos, esses triângulos são semelhantes. Por isso, segue que:
[tex]\qquad \dfrac{AC}{AB}=\dfrac{OC}{OP}[/tex]
donde podemos concluir que:
[tex]\qquad \dfrac{29}{21}=\dfrac{20-r}{r}\\
\qquad 21 \cdot \left(20-r \right)=29r\\
\qquad 420-21r=29r\\
\qquad 50r=420\\
\qquad r=8,4\, cm.[/tex]
Portanto, o raio da semicircunferência é [tex]\fcolorbox{black}{#eee0e5}{$8,4\, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
