(A) Problema para ajudar na escola: Armário em pé

Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)

Matheus comprou um armário novo para seu quarto. Como a altura do quarto é de 2,45 metros, ele comprou um armário que mede 2,4 metros de altura, 2 metros de comprimento e 80 centímetros de profundidade.

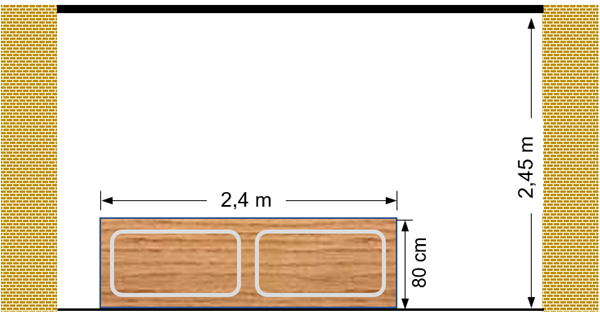
Matheus conseguirá colocar o armário em pé sem que seja preciso desmontá-lo?

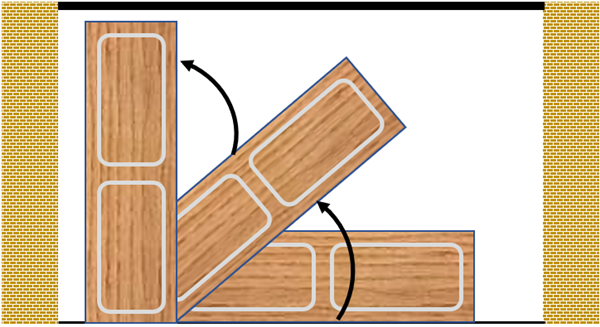
(Problema adaptado do livro Construindo conhecimento em Matemática– Edwaldo Bianchini & Marcos Miani)

Solução

Para ir da posição horizontal (deitado) para a vertical (em pé), o armário deverá passar por posições intermediárias. Em particular, deverá passar pela posição na qual a diagonal representada na figura pelo segmento [tex]\overline{AC}[/tex] fique perpendicular ao chão.

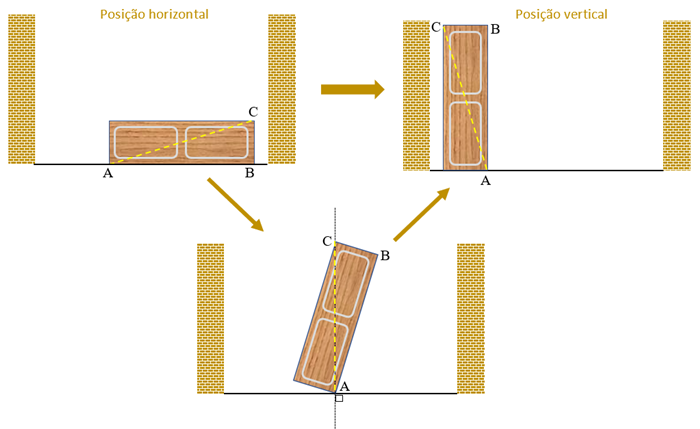
Observe que nessa posição o armário precisa de um espaço entre o teto e o chão de mais de [tex]2,53 \, m[/tex], já que o comprimento [tex]d[/tex] da diagonal do armário é aproximadamente [tex]2,53 \, m.[/tex]
Para encontrarmos o valor de [tex]d[/tex] utilizamos o Teorema de Pitágoras, não sem antes transformar a profundidade do armário de [tex]80[/tex] centímetros para [tex]0,80[/tex] metros:

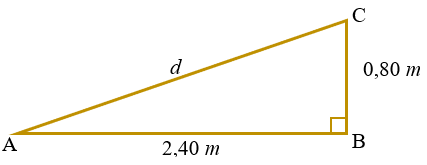
[tex]\qquad d^2=0,8^2+2,4^2\\
\qquad d^2=0,64+5,76\\
\qquad d^2=6,4\\
\qquad d=\sqrt{6,4}[/tex]
[tex] \qquad d \approx 2,53 \, m [/tex], já que [tex]d \gt 0.[/tex]

Pelo exposto, Matheus não conseguirá colocar o armário em pé sem que seja preciso desmontá-lo, pois a altura que ele dispõe para a rotação do armário é de [tex]2,45 \, m.[/tex]

Solução elaborada pelos Moderadores do Blog.

Um applet para ajudar

OBMEP_ srdg, criado com o GeoGebra