Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Fácil)
Ted cortou um quadrado que Meg desenhou em dois retângulos, conforme mostra a figura. Sabendo que a soma dos perímetros desses retângulos é [tex]60 \, \text{cm}[/tex], qual o comprimento do lado do quadrado original?

Solução
Sejam
- [tex]l[/tex] o comprimento em centímetros do quadrado que Meg desenhou e
- [tex]x[/tex] o comprimento em centímetros do lado menor do retângulo esquerdo que Ted cortou (Poderia também ser o lado menor do retângulo direito!).
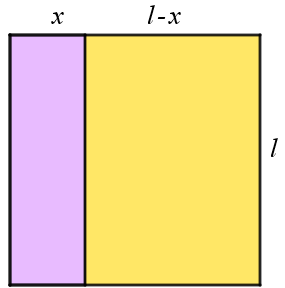
Dessa forma, como a soma dos perímetros dos dois retângulos é [tex]60 \, \text{cm}[/tex], observando a figura acima segue que:
[tex]\qquad \left(x+l+x+l\right) + \left[(l-x)+l+(l-x)+l\right]=60 [/tex]
[tex]\qquad \left(2l+2x\right) + \left( 2l-2x+2l \right)=60 [/tex]
[tex]\qquad 2l+\cancel{2x} +2l-\cancel{2x} +2l =60 [/tex]
[tex]\qquad 6l =60 [/tex]
[tex]\qquad l =10. [/tex]
Portanto, o comprimento do lado do quadrado original era [tex]\fcolorbox{black}{#eee0e5}{$10 \, \text{cm}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
