Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
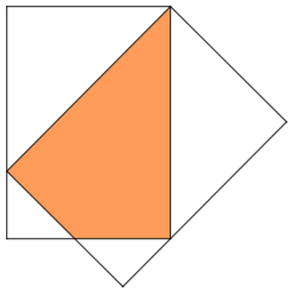
Lívia chegou em casa, depois de um dia exaustivo de aulas, e deixou sobre a sua escrivaninha duas revistas de Biologia, de forma que uma delas cobria parcialmente a capa da outra, conforme ilustra a figura a seguir.
Imagens adaptadas do site Revista da Biologia.
Considerando que as duas revistas são idênticas e possuem formato retangular, verifique se a medida da área de contato das capas, representada colorida na próxima figura, é maior, menor ou igual à metade da medida da área da capa de qualquer uma das duas revistas.
Solução
Sejam [tex]a[/tex] e [tex]b[/tex] os comprimentos dos lados dos retângulos definidos pelas capas das revistas da Lívia. Dessa forma, a área da capa é [tex]\boxed{A_{capa}=a\times b}[/tex] unidades de área.
Por outro lado, observe que a área alaranjada em questão é a soma das áreas [tex]A_1[/tex] e [tex]A_2[/tex] indicadas na figura a seguir.
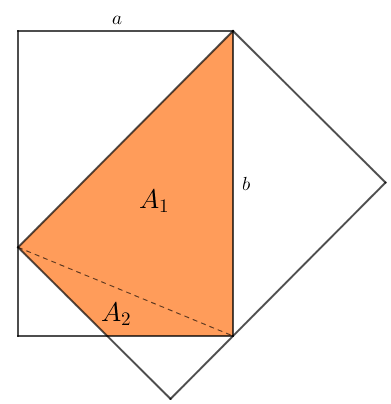
Assim, essa área alaranjada é dada por [tex]\textcolor{#F87217}{A_{al}}=\dfrac{a\times b}{2}+A_2[/tex]. Como [tex]A_2 \gt 0[/tex], então a área alaranjada [tex]\textcolor{#F87217}{A_{al}}[/tex] é maior do que [tex]\dfrac{a\times b}{2}[/tex], que é metade da área de cada capa. Observe:
[tex]\qquad \textcolor{#F87217}{A_{al}}=A_1+A_2\\
\qquad \textcolor{#F87217}{A_{al}}=\dfrac{a\times b}{2}+A_2\\
\qquad \textcolor{#F87217}{A_{al}} \gt \dfrac{a\times b}{2}\\
\qquad \fcolorbox{black}{#eee0e5}{$\textcolor{#F87217}{A_{al}} \gt \dfrac{A_{capa}}{2}$}\, .\\
[/tex]
Portanto, a medida da área de contato das capas das revistas é maior que a metade da medida da área da capa de qualquer uma das duas revistas.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |