.Problema: Paralelogramo

Problema
(Indicado a partir do 1º ano do E. M.)

Um ponto F é tomado no prolongamento do lado AD de um paralelogramo ABCD.
O segmento BF intercepta a diagonal AC no ponto E e o lado DC em G.
Se EF=32 cm e GF=24 cm, determine a medida de BE.

Solução

Observe a figura a seguir, construída a partir dos dados do problema.

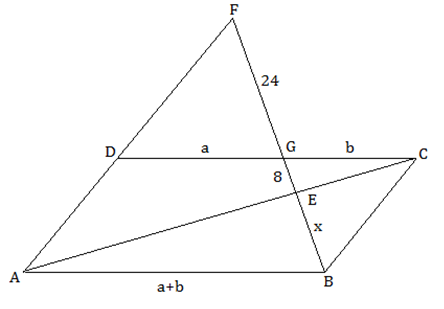
Paralelogramo

Da semelhança dos triângulos [tex]DGF[/tex] e [tex]CGB[/tex] (Você saberia justificar tal semelhança?), podemos escrever
[tex]\quad \quad \dfrac{a}{b}=\dfrac{24}{8+x}~.\qquad (I)[/tex]

Agora, da semelhança dos triângulos [tex]CEG[/tex] e [tex]AEB[/tex] (Você saberia justificar tal semelhança?), podemos escrever
[tex]\quad \quad \dfrac{b}{a+b}=\dfrac{8}{x}~. \qquad (II)[/tex]

Após resolver o sistema formados pelas equações [tex](I)[/tex] e [tex](II)[/tex], encontramos [tex]x=16[/tex].
Portanto, o comprimento do segmento [tex]BE[/tex] é [tex]16\,cm[/tex].

De (II) temos que
[tex]\quad \quad \dfrac{a+b}{b}=\dfrac{x}{8}[/tex]
e assim
[tex]\quad \quad \dfrac{a}{b}+1=\dfrac{x}{8}[/tex]
ou ainda
[tex]\quad \quad \dfrac{a}{b}=\dfrac{x}{8}-1[/tex].
Então, por (I),
[tex]\quad \quad \dfrac{24}{8+x}=\dfrac{x-8}{8}[/tex],
e assim:
[tex]\quad \quad 24\times 8=(x-8)\, (x+8)[/tex]
[tex]\quad \quad 24\times 8=x^2-64[/tex]
[tex]\quad \quad x^2=192+64=256[/tex]
[tex]\quad \quad x=\pm 16[/tex].
Como [tex]x[/tex] representa um comprimento, [tex]\fbox{$x=16$}[/tex].

Solução elaborada pelos Moderadores do Blog.

Link permanente para este artigo: http://clubes.obmep.org.br/blog/problema-paralelogramo/

Deixe uma resposta