Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Fácil)
Maria Emília comprou uma caixa na forma de um paralelepípedo retangular de comprimento [tex] 42 \, \text{cm}\, [/tex] e de largura [tex] \, 34 \, \text{cm}[/tex], para embalar o presente que ela comprou para sua mãe.
Para decorar o pacote de acordo com a figura abaixo, ela utilizou [tex] 2,90 \, m[/tex] de fita vermelha, dos quais [tex]30 \, \text{cm}[/tex] foram para a confecção do nó e do laço.
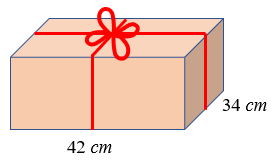
Qual a altura da caixa?
Solução
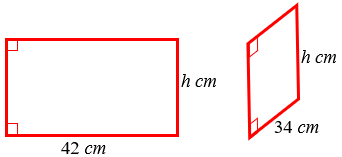
Para resolver o problema, precisaremos calcular a soma [tex]S[/tex] das medidas de todos os lados de cada um dos dois retângulos definidos pela fita vermelha que Maria Emília utilizou. Para isso, vamos denotar a altura em centímetros da caixa por [tex]h[/tex]. Assim:
[tex]\qquad S= \left(h+42+h+42\right)+\left(h+34+h+34\right)[/tex]
[tex]\qquad S=152+4h.[/tex]
Mas vamos lembrar que Maria Emília utilizou para decorar o pacote [tex] 2,90 \, m[/tex] de fita, dos quais [tex]30 \, \text{cm}[/tex] foram utilizados na confecção do nó e do laço; portanto, transformando os [tex] 2,90 \, m[/tex] em centímetros, segue que:
[tex]\qquad 290=(152+4h)+30[/tex]
[tex]\qquad 290=182+4h[/tex]
[tex]\qquad 290-182=4h[/tex]
[tex]\qquad 108=4h[/tex]
[tex]\qquad h=27 \, \text{cm}.[/tex]
Então, a altura da caixa utilizada pela Maria Emília para embalar o presente que ela comprou para sua mãe é [tex] \, \fcolorbox{black}{#eee0e5}{$ 27 \, \text{cm}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
