Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
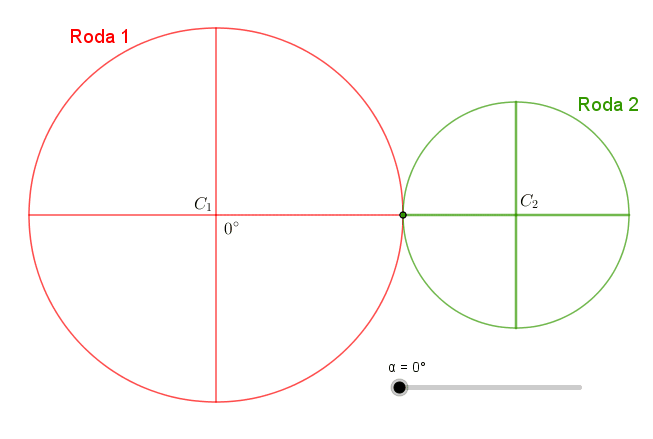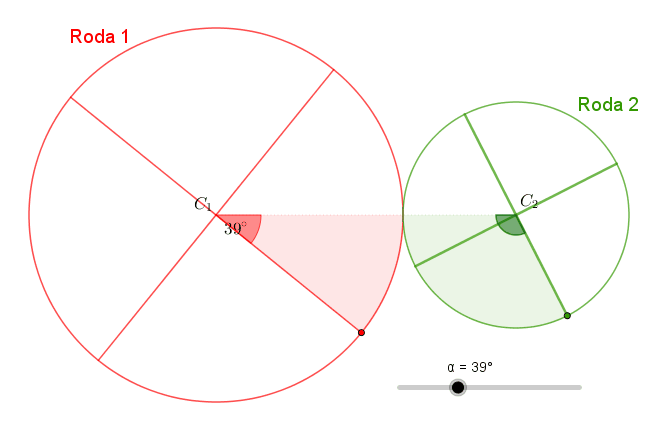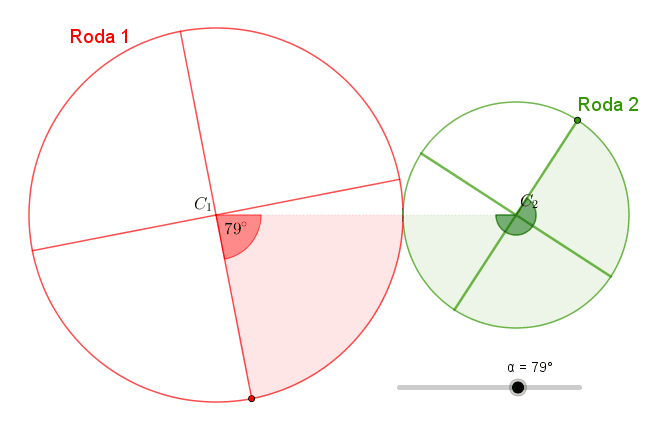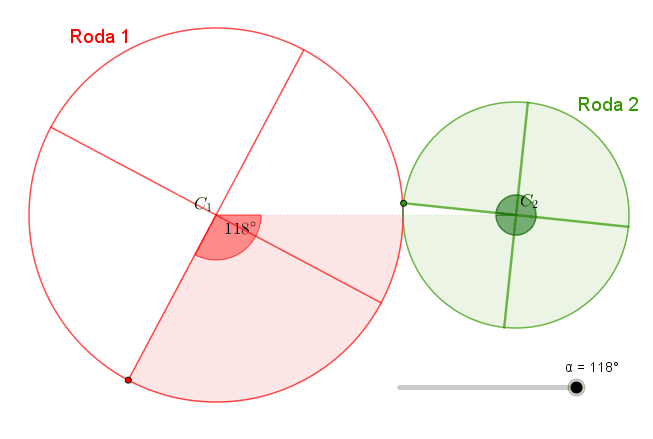
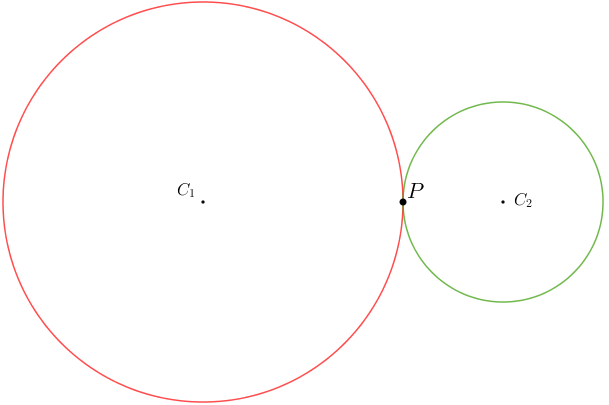
(ONEM 2009 – Adaptado) Na figura vemos as Rodas 1 e 2 girando.
Observe que, enquanto a Roda 1 gira [tex] 120^{\circ}[/tex], a Roda 2 gira [tex]2\pi [/tex] radianos.
Quantos centímetros mede o raio da Roda 1, se a distância entre os dois centros [tex]C_1 [/tex] e [tex]C_2 [/tex] é [tex]160\, [/tex]cm?
Considere que as circunferências que definem as duas rodas são tangentes externas.

Ajuda
A um arco de circunferência podemos associar duas medidas distintas:
✐ a sua medida angular (em graus ou radianos), [tex]\alpha[/tex];
✐ a sua medida linear (em unidades de comprimento), [tex]c[/tex].
Conhecida uma delas, a outra pode ser obtida a partir da medida angular e do comprimento da circunferência que define o arco por meio de uma regra de três simples:
| [tex]2\pi \, r[/tex] | ————————————– | [tex]360^\circ[/tex] |
| [tex]c[/tex] | ————————————– | [tex]\alpha[/tex] |
Se você não se lembra disso, não faz mal: clique AQUI.
Solução
Após um giro de [tex] 120^{\circ}[/tex] da Roda 1 a partir do ponto de tangência [tex]P[/tex], obtemos a imagem abaixo.
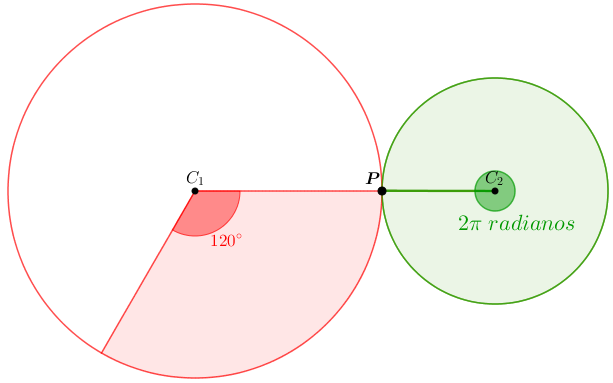
Como a Roda 1 girou [tex] 120^{\circ}[/tex] e a Roda 2 girou [tex]2\pi[/tex] radianos, a partir do ponto [tex]P[/tex] ficam definidos um arco na circunferência da Roda 1 cuja medida angular é [tex] 120^{\circ}[/tex] ou [tex] \frac{2\pi}{3}[/tex] radianos e um arco na circunferência da Roda 2 cuja medida angular é [tex] 360^{\circ}[/tex] ou [tex] 2\pi[/tex] radianos.
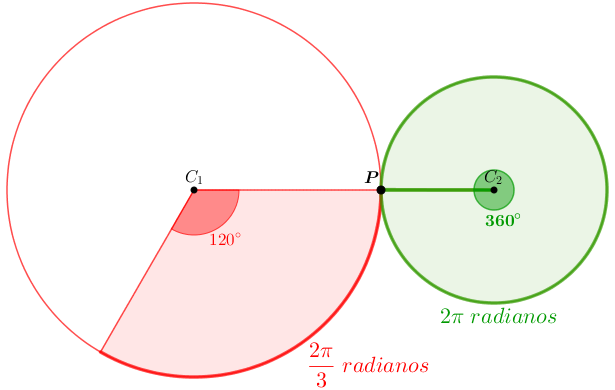
Mas, observe que:
- a cada giro de [tex] 120^{\circ}[/tex] da Roda 1, cada ponto do arco de [tex] \frac{2\pi}{3}[/tex] radianos esteve em contato com o ponto de tangência [tex]P,[/tex]
- a cada giro de [tex] 360^{\circ}[/tex] da Roda 2, cada ponto do arco de [tex] 2\pi[/tex] radianos esteve em contato com o ponto de tangência [tex]P,[/tex]
portanto, os dois arcos têm o mesmo comprimento, ou seja, a mesma medida linear. [tex]\qquad \textcolor{#800000}{(i)}[/tex]
Se você não conseguiu visualizar as duas afirmações que deram origem à conclusão de que os arcos descritos nas duas rodas têm o mesmo comprimento, utilize o applet abaixo. É só esperar o aplicativo carregar, movimentar manualmente os botões identificados com as letras gregas [tex]\textcolor{red}{\alpha}[/tex] e [tex]\textcolor{#009900}{\theta}[/tex] e observar.
OBMEP_srdg, criado com o GeoGebra
Vamos, então, calcular as medidas lineares dos dois arcos. Para isso, considere [tex] r_1[/tex] e [tex] r_2[/tex] os raios das circunferências, conforme ilustra a figura a seguir, e sejam [tex] c_1[/tex] e [tex] c_2[/tex] os comprimentos em centímetros dos arcos de [tex] \frac{2\pi}{3}[/tex] radianos e [tex] 2\pi[/tex] radianos, respectivamente.
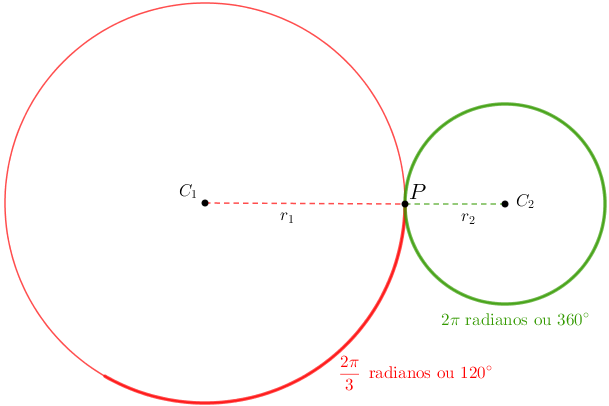
- Medida linear [tex]c_1[/tex]
- Medida linear [tex]c_2[/tex]
Usando a regrinha de três mostrada na Ajuda, segue que:
[tex] \begin{array}{c c c}
2\pi\, r_1 &\text{————–}&360^\circ\\
c_1 &\text{————–}& 120^\circ
\end{array}[/tex]
donde
[tex]\qquad c_1=2\pi\, r_1 \times \dfrac{120^\circ}{360^\circ}=\dfrac{2\pi\, r_1}{3}.[/tex]
Usando a regrinha de três mostrada na Ajuda, segue que:
[tex] \begin{array}{c c c}
2\pi\, r_2 &\text{————–}&360^\circ\\
c_2 &\text{————–}& 360^\circ
\end{array}[/tex]
donde
[tex]\qquad c_2=2\pi\, r_2 \times \dfrac{360^\circ}{360^\circ}=2\pi\, r_2.[/tex]
Mas, por [tex]\textcolor{#800000}{(i)}[/tex], [tex]c_1=c_2[/tex], logo:
[tex]\qquad \dfrac{2\pi\, r_1}{3}=2\pi\, r_2[/tex]
e, assim,
[tex]\qquad \boxed{ r_1=3r_2}.\qquad \textcolor{#800000}{(ii)}[/tex]
Mas lembre-se de que a distância entre os dois centros [tex]C_1 [/tex] e [tex]C_2 [/tex] é [tex]160\, [/tex]cm; portanto:
[tex]\qquad \boxed{ r_1+r_2=160}.\qquad \textcolor{#800000}{(iii)}[/tex]
Veja que, de [tex]\textcolor{#800000}{(ii)}[/tex] e [tex]\textcolor{#800000}{(iii)}[/tex], segue que:
[tex]\qquad r_1+r_2=160[/tex]
[tex]\qquad 3r_2+r_2=160[/tex]
[tex]\qquad 4r_2=160[/tex]
[tex]\qquad \fcolorbox{black}{#d7d7d7}{$r_2=40$}.[/tex]
Substituindo esse valor em [tex]\textcolor{#800000}{(ii)}[/tex], obtemos que [tex]\fcolorbox{black}{#d7d7d7}{$r_1=120$}.[/tex]
Então, o raio da Roda 1 é [tex]\fcolorbox{black}{#fbb}{$120\text{ cm}$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
