Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Fácil)
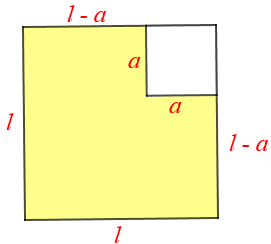
A figura abaixo mostra dois quadrados: um interno e outro externo. O perímetro da região colorida de amarelo mostrada na figura é [tex]36 \, \text{cm}. [/tex]
Qual a área do quadrado externo? Apresente a resposta em [tex]\text{m}^2 \, .[/tex]

Solução
Suponhamos que [tex]l \, [/tex] e [tex] \, a \, [/tex] sejam os comprimentos, em centímetros, dos lados do quadrado externo e do quadrado interno, respectivamente.
Assim, observando a figura abaixo, percebemos facilmente que o perímetro [tex]P[/tex] da região colorida de amarelo é dado por:
[tex] P=l+l+(l-a)+a+a+(l-a).[/tex]
Mas, de acordo com o enunciado do problema, [tex]P=36 \, \text{cm}[/tex]; assim, segue que:
[tex]l+l+(l-a)+a+a+(l-a)=36[/tex]
[tex]4l+2a-2a=36[/tex]
[tex]4l=36[/tex]
[tex]l=9 \, \text{cm}.[/tex]
Dessa forma, concluímos que a área [tex]A[/tex] do quadrado externo é [tex]A=9^2=81 \, \text{cm}^2.[/tex]
Para finalizarmos a solução do problema, só precisamos converter [tex]81 \, \text{cm}^2 \, [/tex] em [tex]\text{m}^2 \, [/tex] e, para isso, o esqueminha abaixo pode ajudar!
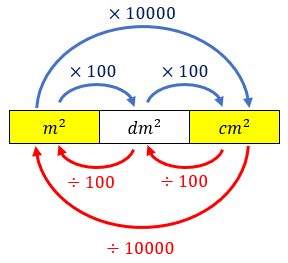
- Área do quadrado externo em [tex]\text{m}^2:[/tex]
[tex]\qquad 81 \, \text{cm}^2 \div 10000 \longmapsto\fcolorbox{black}{#eee0e5}{$0,0081 \, \text{m}^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
