Problema
(Indicado a partir do 9º ano do E. F.)
(ITA 1990) Há muito tempo, quando poucas pessoas eram versadas na arte de contar, houve uma grande tempestade no oceano. Um navio, colhido pelo tufão, foi salvo graças ao trabalho excepcional de dois marinheiros. Terminada a borrasca, o capitão, decidido a recompensar seus dois comandados pelo serviço bem executado, anunciou que dividiria entre eles no dia seguinte o conteúdo de um pequeno baú com moedas de ouro, tendo encarregado o seu imediato desta tarefa. Acontece que os dois marinheiros eram muito amigos e, querendo evitar o constrangimento de uma partilha pública, um deles teve a ideia na madrugada de pegar a sua parte do prêmio. Indo ao baú, este marinheiro separou as moedas em dois grupos idênticos e, para sua surpresa, sobrou uma moeda. Não sabendo como proceder, jogou-a ao mar para agradecer aos deuses a sua sobrevivência e pegou a parte que lhe cabia. Porém, mais tarde o segundo marinheiro teve exatamente a mesma ideia. Indo ao baú, ele separou as moedas em dois montes iguais e, para surpresa sua, sobrou uma moeda. Jogou-a ao mar como agradecimento pela sua sorte e tomou a parte que lhe cabia da recompensa. Pela manhã os dois marinheiros se sentiram constrangidos em comunicar o procedimento noturno. Assim, o imediato separou as moedas em dois grupos e verificou que sobrava uma. Deu a cada marinheiro a sua parte do prêmio e tomou para si a moeda restante como paga pelos seus cálculos.
Sabendo-se que a razão entre as moedas ganhas pelo primeiro e pelo segundo marinheiros foi de [tex]\dfrac{29}{17}[/tex], determine a quantidade mínima de moedas que havia originalmente no baú.
Solução 1
Eram dois marinheiros, o 1º marinheiro (1º M) e o 2º marinheiro (2º M).
O 1ºM foi ao baú pegou “x” moedas dividindo-as em duas partes jogou uma fora, ficou com a metade de “x” menos ½, ou seja,
x/2- 1/(2)=(x-1)/2•, (1/2 representa a moeda que foi joga fora na sobra da divisão),
ficando no baú x/2-1/(2)•.
O 2ºM foi ao baú e fez o mesmo só que no baú havia x/2- 1/(2) (moedas), ao retirar a metade também jogou uma moeda fora ficando com (x-3)/4•, verificado através dos cálculos e deixando a mesma quantidade no baú,
((x-1)/2)/(2/1)-1/(2)=(x-1)/4-1/(2)=(x-1)/4-2/(4)=(x-3)/4•.
Em seguida, o imediato pegou o baú separou as moedas em duas partes iguais, sobrou uma moeda que pegou para si e cada marinheiro recebeu
((x-3)/4)/(2/1)-1/(2)=(x-3)/4-1/(2)=(x-3)/8-4/(8)=(x-7)/8•.
Pelo fato ocorrido o 1º marinheiro recebeu
(x-1)/2+(x-7)/8=(4x-4)/8+(x-7)/8=(5x-11)/8
e o 2º marinheiro recebeu
(x-3)/4+(x-7)/8=(2x-6)/8+(x-7)/8=(3x-13)/8.
Sabendo que a razão entre as moedas ganhas pelo 1º M e pelo 2º M foi de 29/(17 )•, temos:
→((5x-11)/8)/((3x-13)/8) = 29/(17 )
→ (8(5x-11) )/(8(3x-13) ) = 29/(17 )
→ 29(3x – 13) = 17(5x – 11)
→ 87x – 377 = 85x -187
→ 87x – 85x = -187 + 377
→ 2x = 190
→ x = 95.
Portanto, no baú havia 95 moedas.
Solução elaborada pelo Clube MIRIM APRENDIZ.
Solução 2
Suponha que [tex] x [/tex] seja a quantidade de moedas recebidas por cada um dos marinheiros, quando da divisão feita pelo imediato, e observe o esquema mostrado a seguir.
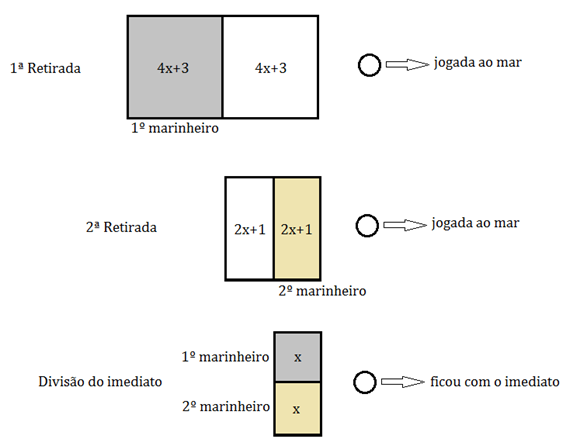
Como a razão entre as moedas ganhas pelo primeiro e pelo segundo marinheiros foi de [tex]\dfrac{29}{17}[/tex], temos que
[tex]\quad \quad \dfrac{(4x+3)+x}{(2x+1)+x}=\dfrac{29}{17}[/tex]
donde concluímos que [tex]\; x=11\;.[/tex]
Finalmente, a quantidade mínima de moedas do baú era
[tex]\qquad (4x+3)+(4x+3)+(1)=8x+7=\fcolorbox{black}{#eee0e5}{$95$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog .
