Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
O esquema abaixo mostra a multiplicação entre um número de três algarismos e um número de dois algarismos.
Se cada quadradinho representa um algarismo, calcule o resultado da multiplicação.
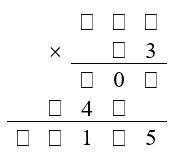
Solução
Seja [tex]a[/tex] o algarismo das unidades do número que aparece na primeira linha do esquema da nossa multiplicação.
- Observe que o primeiro produto obtido no esquema apresentado termina em [tex]5[/tex].
[tex]\begin{array}{c c c c c}
& & \Box & \Box & \textcolor{red}{a}\\
& \times& & \Box & \textcolor{red}{3}\\
\hline
& & \Box & 0 &\textcolor{red}{5}\\
& \Box & 4 & \Box & & \\
\hline
\Box & \Box & 1 & \Box & \textcolor{red}{5}
\end{array}\qquad [/tex]
Dessa forma, o produto [tex] \textcolor{red}{3 \times a}[/tex] termina em [tex] \textcolor{red}{5}[/tex] e [tex] \textcolor{red}{ a}[/tex] é um algarismo; então, [tex] \textcolor{red}{a=5}.[/tex]
Ficamos, então, com um esquema melhor:
[tex]\qquad \qquad \begin{array}{c c c c c}
& & & \underline{1} & \\
& & \Box & \Box & 5\\
& \times& & \Box & 3\\
\hline
& & \Box & 0 & 5\\
& \Box & 4 & \Box & & \\
\hline
\Box & \Box & 1 & \Box & 5
\end{array}\qquad [/tex]
Seja [tex]b[/tex] o algarismo das dezenas do número que aparece na primeira linha do esquema da nossa multiplicação.
- No segundo passo do algoritmo da multiplicação fazemos um produto e uma soma e o número que obtemos termina em [tex]0[/tex].
[tex] \begin{array}{c c c c c}
& & & \underline{\textcolor{red}{1}} & \\
& & \Box & \textcolor{red}{b} & 5\\
& \times& & \Box & \textcolor{red}{3}\\
\hline
& & \Box & \textcolor{red}{0} & 5\\
& \Box & 4 & \Box & & \\
\hline
\Box & \Box & 1 & \Box & 5
\end{array}\qquad [/tex]
Dessa forma, o número [tex] \textcolor{red}{3 \times b+1}[/tex] termina em [tex] \textcolor{red}{0}[/tex] e sendo [tex] \textcolor{red}{ b}[/tex] um algarismo; então, [tex] \textcolor{red}{b=3}.[/tex]
Ficamos, então, com o seguinte esquema:
[tex]\qquad \qquad \begin{array}{c c c c c}
& & \underline{1} & \underline{1} & \\
& & \Box & 3 & 5\\
& \times& & \Box & 3\\
\hline
& & \Box & 0 & 5\\
& \Box & 4 & \Box & & \\
\hline
\Box & \Box & 1 & \Box & 5
\end{array}\qquad [/tex]
Agora, seja [tex]c[/tex] o algarismo das centenas do número que aparece na terceira linha do esquema da nossa multiplicação.
- Observe que o algarismo [tex]c[/tex] somado com [tex]4[/tex] produz um número que termina em [tex]1.[/tex]
[tex] \begin{array}{c c c c c}
& & \underline{1} & \underline{1} & \\
& & \Box & 3 & 5\\
& \times& & \Box & 3\\
\hline
& & \textcolor{red}{c} & 0 & 5\\
& \Box & \textcolor{red}{4} & \Box & & \\
\hline
\Box & \Box & \textcolor{red}{1} & \Box & 5
\end{array}\qquad [/tex]
Então, a única alternativa que temos é [tex] \textcolor{red}{c=7}[/tex]. Com isso o número que aparece na terceira linha está completamente determinado e ficamos com este esquema:
[tex]\qquad \qquad \begin{array}{c c c c c}
& & \underline{1} & \underline{1} & \\
& & \Box & 3 & 5\\
& \times& & \Box & 3\\
\hline
& & 7 & 0 & 5\\
& \Box & 4 & \Box & & \\
\hline
\Box & \Box & 1 & \Box & 5
\end{array}\qquad [/tex]
Denotaremos por [tex]d[/tex] o algarismo das centenas do número que aparece na primeira linha.
- Perceba que [tex]\textcolor{red}{3 \times d35=705}[/tex].
[tex]\begin{array}{c c c c c}
& & \textcolor{red}{d} & \textcolor{red}{3} & \textcolor{red}{5}\\
& \times& & \Box & \textcolor{red}{3}\\
\hline
& & \textcolor{red}{7} & \textcolor{red}{0} & \textcolor{red}{5}\\
& \Box & 4 & \Box & & \\
\hline
\Box & \Box & 1 & \Box & 5
\end{array}\qquad [/tex]
Logo, [tex]d35=705 \div3=235[/tex] e, portanto, [tex]\textcolor{red}{d=2}.[/tex]
Com mais essa informação, nossa multiplicação fica assim:
[tex]\qquad \qquad \begin{array}{c c c c c}
& & 2 & 3 & 5\\
& \times& & \Box & 3\\
\hline
& & 7 & 0 & 5\\
& \Box & 4 & \Box & & \\
\hline
\Box & \Box & 1 & \Box & 5
\end{array}\qquad [/tex]
Vamos denotar por [tex]e[/tex] o algarismo das dezenas do número da segunda linha.
- Praticamente finalizaremos o problema.
[tex] \begin{array}{c c c c c}
& & \textcolor{red}{2} & \textcolor{red}{3} &\textcolor{red}{ 5}\\
& \times& & \textcolor{red}{e} & 3\\
\hline
& & 7 & 0 & 5\\
& \Box & \textcolor{red}{4} & \Box & & \\
\hline
\Box & \Box & 1 & \Box & 5
\end{array}\qquad [/tex]
Observe que [tex]e \times 235[/tex] resulta em um número de três algarismos, cujo algarismo central é [tex]\textcolor{red}{4}.[/tex]
Mas só existem três múltiplos de [tex] 235[/tex] com três algarismos:
[tex] \quad 235=235 \times 1\; ;\quad 470=235 \times 2\; ;\; 705=235 \times 3\; ;\; \boxed{940=235 \times \textcolor{red}{4}}\,.[/tex]
Como podemos ver, desses, apenas o número [tex]940[/tex] satisfaz a condição de o algarismo central ser [tex]4[/tex]. Assim, [tex]\textcolor{red}{e=4}[/tex] e fechamos a nossa multiplicação, já que, com essas informações, concluímos que o esquema apresentado no problema é o algoritmo da multiplicação [tex]235 \times 43.[/tex]
[tex]\qquad \qquad \begin{array}{c c c c c}
& & 2 & 3 & 5\\
& \times& & 4 & 3\\
\hline
& & 7 & 0 & 5\\
& 9 & 4 & 0 & & \\
\hline
1 & 0 & 1 & 0 & 5
\end{array}\qquad [/tex]
Dessa forma, o resultado da multiplicação é [tex]\, \fcolorbox{black}{#eee0e5}{$10105$}[/tex] .
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
