Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
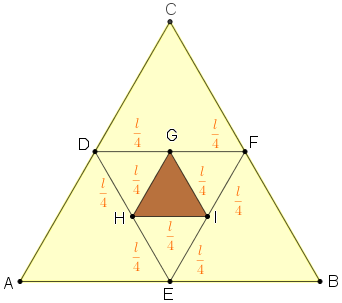
(ONEM – 2011) O triângulo [tex]ABC[/tex] mostrado na figura é equilátero e os pontos [tex]D, E, F[/tex] são pontos médios dos segmentos [tex]\overline{CA}[/tex], [tex]\overline{AB}[/tex], [tex]\overline{BC}[/tex], respectivamente.
Por outro lado, [tex]G, H, I[/tex] são pontos médios dos segmentos [tex]\overline{FD}[/tex], [tex]\overline{DE}[/tex], [tex]\overline{EF}[/tex], respectivamente.
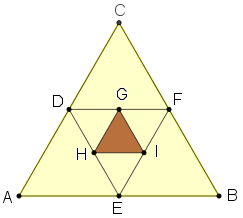
Nessas condições, a área do triângulo [tex]GHI[/tex] corresponde a que porcentagem da área do triângulo [tex]ABC[/tex]?

Lembretes
(1) Caso de congruência L.A.L. (lado – ângulo – lado): Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes.
(2) Os ângulos da base de um triângulo isósceles são congruentes.
(3) Caso de congruência L.L.L. (lado – lado- lado): Se dois triângulos têm ordenadamente congruentes os três lados, então estes triângulos são congruentes.
(Se você não se lembra desses resultados, clique AQUI.)
Solução
Observe, inicialmente, que
- como o triângulo [tex]ABC[/tex] é equilátero, os segmentos [tex]\overline{AB}~[/tex], [tex]\overline{BC}~[/tex] e [tex]~\overline{CA}[/tex] têm o mesmo comprimento, digamos [tex]l[/tex];
- como [tex]D, E, F[/tex] são pontos médios dos segmentos [tex]\overline{CA}[/tex], [tex]\overline{AB}[/tex] e [tex]\overline{BC}[/tex], os segmentos [tex]\overline{AE}~[/tex], [tex]\overline{EB}~[/tex], [tex]\overline{BF}~[/tex], [tex]\overline{FC}~[/tex], [tex]\overline{CD}~[/tex] e [tex]\overline{DA}~[/tex] têm comprimentos iguais a [tex]\frac{l}{2}~.[/tex]
- como [tex]\Delta ABC[/tex] é um triângulo equilátero, cada um de seus ângulos internos mede [tex]60^{\circ}~.[/tex]
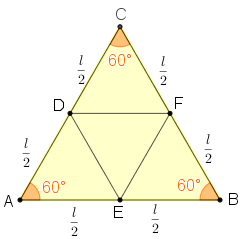
Com isso, pelo Lembrete (1), os triângulos [tex]DAE~[/tex], [tex]EBF~[/tex] e [tex]FCD[/tex] são congruentes.
Mais do que isso, como esses triângulos são isósceles, pelo Lembrete (2), seus ângulos de base têm a mesma medida. Assim, como a medida do terceiro ângulo de cada triângulo é [tex]60^{\circ}~[/tex], a medida de cada ângulo de base será [tex]\dfrac{180^{\circ}-60^{\circ}}{2}=60^{\circ}[/tex] e, então, os três triângulos são equiláteros.
Portanto, na realidade, temos quatro triângulos congruentes: [tex]DAE~[/tex], [tex]EBF~[/tex], [tex]FCD~[/tex] e [tex]DEF~.[/tex]
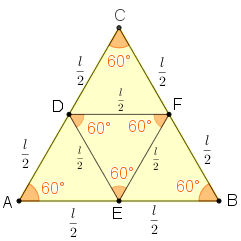
Como os quatro triângulos [tex]DAE~[/tex], [tex]EBF~[/tex], [tex]FCD~[/tex] e [tex]DEF~[/tex] têm a mesma área, se denotarmos as áreas dos triângulos [tex]DEF~[/tex] e [tex]~ABC[/tex] por, respectivamente, [tex][DEF]~[/tex] e [tex]~[ABC][/tex], segue que:
[tex]\qquad [DEF]=\dfrac{[ABC]}{4}\qquad \textcolor{#800000}{(i)}~.[/tex]
De maneira análoga, mantendo a notação [tex][ ~~][/tex] para indicar áreas, podemos concluir que:
[tex]\qquad [GHI]=\dfrac{[DEF]}{4}\qquad \textcolor{#800000}{(ii)}~[/tex],
assim, de [tex]\textcolor{#800000}{(i)}~[/tex] e de [tex]\textcolor{#800000}{(ii)}~[/tex], segue que:
[tex]\qquad [GHI]\stackrel{\textcolor{#800000}{(ii)}}{=}\dfrac{[DEF]}{4}\stackrel{\textcolor{#800000}{(i)}}{=}\dfrac{\dfrac{[ABC]}{4}}{4}=\dfrac{[ABC]}{16}~,[/tex]
ou seja, [tex][GHI]=\dfrac{[ABC]}{16}~.[/tex]
Para expressarmos essa relação entre áreas percentualmente, basta fazermos uma regrinha de três simples. Observe:
| [tex][ABC][/tex] | —————————- | [tex]100\%[/tex] |
| [tex][GHI][/tex] | —————————- | [tex]?[/tex] |
Substituindo a relação [tex][GHI]=\dfrac{[ABC]}{16}~[/tex], segue que
| [tex][ABC][/tex] | —————————- | [tex]100\%[/tex] |
| [tex]\dfrac{[ABC]}{16}[/tex] | —————————- | [tex]?[/tex] |
e, assim,
[tex]\qquad ?=\dfrac{100\% \times \dfrac{[ABC]}{16}}{[ABC]}=\dfrac{100\% \times\cancel{[ABC]}}{16 \times\cancel{[ABC]}}=\dfrac{100}{16}\%~.[/tex]
Logo, a área do triângulo [tex]GHI[/tex] corresponde a [tex]\fcolorbox{black}{#eee0e5}{$6,25\%$}~[/tex] da área do triângulo [tex]ABC.[/tex]
Se você não conseguiu obter a equação [tex]\textcolor{#800000}{(ii)},~[GHI]=\dfrac{[DEF]}{4}~[/tex], clique no botão abaixo e acompanhe a dedução.
Como já sabemos que os ângulos com vértices em [tex]D, E, F[/tex] medem [tex]60^{\circ}~[/tex], então pelo Lembrete (1) podemos concluir que os triângulos [tex]DHG~[/tex], [tex]EIH~[/tex] e [tex]FGI[/tex] são congruentes.
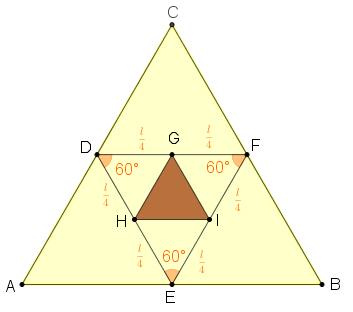
Por outro lado, veja que esses três triângulos são isósceles; logo, pelo Lembrete (2), seus ângulos de base têm a mesma medida. Com isso, como a medida do terceiro ângulo de cada triângulo é [tex]60^{\circ}~[/tex], a medida de cada ângulo de base será [tex]\dfrac{180^{\circ}-60^{\circ}}{2}=60^{\circ}.[/tex] Assim, os três triângulos [tex]DHG~[/tex], [tex]EIH~[/tex] e [tex]FGI[/tex] são equiláteros, e, pelo Lembrete (3), os triângulos [tex]DHG~[/tex], [tex]EIH~[/tex], [tex]FGI~[/tex] e [tex]GHI[/tex] são congruentes.
Como os triângulos [tex]DHG~[/tex], [tex]EIH~[/tex], [tex]FGI~[/tex] e [tex]GHI[/tex] têm a mesma área, se denotarmos as áreas dos triângulos [tex]DEF~[/tex] e [tex]~GHI[/tex] por, respectivamente, [tex][DEF]~[/tex] e [tex]~[GHI][/tex], segue que [tex]\boxed{[GHI]=\dfrac{[DEF]}{4}}~.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
