Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
Montamos um grande cubo, a partir de [tex]125[/tex] cubinhos brancos de mesmo tamanho, e pintamos de azul as seis faces do cubo grande.
Em seguida, separamos o cubo grande nos [tex]125[/tex] cubinhos iniciais.
Quantos cubos pequenos terão tinta azul em:
(a) exatamente três faces?
(b) exatamente duas faces?
(c) apenas uma face?
(d) nenhuma face?

Um applet para iniciar
Se você não conseguiu resolver o problema a partir de um cubo formado [tex]125[/tex] cubinhos, antes de ler a solução, pense como seria o problema se o cubo grande fosse formado a partir de [tex]27[/tex] cubinhos.
Para ajudar, utilize o applet abaixo.
Instruções:
(1) Espere o arquivo carregar completamente.
(2) Para mover o cubo, clique em qualquer lugar na telinha do applet, mantenha o mouse pressionado e movimente-o.
(3) Se o cubo começar a girar sozinho, é só clicar em qualquer lugar na telinha do applet para ele parar.
(4) Rolando o botão de scroll (rodinha usada para rolamento) do mouse, você pode aumentar ou diminuir o cubo.
Para carregar o applet, clique AQUI
OBMEP_ srdg, criado com o GeoGebra
Solução
Vamos às respostas para o cubo formado por [tex]125[/tex] cubinhos.
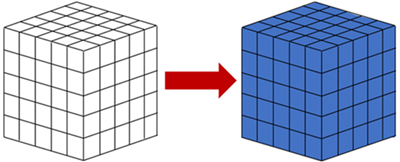
(a) Os cubinhos com três faces pintadas são aqueles que estão nos cantos do cubo grande.
Portanto, depois de separados, [tex]\fcolorbox{black}{#eee0e5}{$8$}[/tex] cubinhos terão tinta azul em exatamente três faces.
(b) Os cubinhos com duas faces pintadas são aqueles com uma aresta contida no meio de cada aresta do cubo grande.
Assim, depois de separados, [tex]\fcolorbox{black}{#eee0e5}{$3 \times 12=36$}[/tex] cubinhos terão tinta azul em exatamente duas faces.
(c) Os cubinhos com apenas uma face pintada são aqueles que estão no centro de cada face do cubo grande.
Logo, depois de separados, [tex]\fcolorbox{black}{#eee0e5}{$9 \times 6=54$}[/tex] cubinhos terão tinta azul em exatamente uma de suas faces.
Você pode visualizar esses três primeiros resultados, utilizando o applet abaixo.
Instruções:
(1) Espere o arquivo carregar completamente.
(2) Para mover o cubo, clique em qualquer lugar na telinha do applet, mantenha o mouse pressionado e movimente-o.
(3) Se o cubo começar a girar sozinho, é só clicar em qualquer lugar na telinha do applet para ele parar.
(4) Rolando o botão de scroll (rodinha usada para rolamento) do mouse, você pode aumentar ou diminuir o cubo.
Legenda:
– Os cubinhos com três faces pintadas são os coloridos de verde.
– Os cubinhos com duas faces pintadas são os coloridos de rosa.
– Os cubinhos com uma face pintada são os coloridos de azul.
Para carregar o applet, clique AQUI
OBMEP_ srdg, criado com o GeoGebra
(d) Os cubinhos sem faces pintadas são aqueles que estão no interior do cubo grande. A quantidade desses cubinhos pode ser obtida fazendo-se a diferença entre o total de cubinhos e o número de cubinhos com alguma face pintada:
[tex] 125-(8+36+54)=125-98=27[/tex] .
Dessa forma, depois de separados, [tex]\fcolorbox{black}{#eee0e5}{$27$}[/tex] cubinhos não terão tinta azul em qualquer uma de suas faces.
Você pode utilizar o applet abaixo para observar que o bloco de cubinhos sem faces pintadas define um cubo formado por [tex]27[/tex] cubinhos, do tipo daquele trabalhado no primeiro applet desta página.
Instruções:
(1) Espere o arquivo carregar completamente.
(2) Para mover o cubo, clique em qualquer lugar na telinha do applet, mantenha o mouse pressionado e movimente-o.
(3) Se o cubo começar a girar sozinho, é só clicar em qualquer lugar na telinha do applet para ele parar.
(4) Rolando o botão de scroll (rodinha usada para rolamento) do mouse, você pode aumentar ou diminuir o cubo.
Para carregar o applet, clique AQUI
OBMEP_ srdg, criado com o GeoGebra
Solução elaborada pelos Moderadores do Blog.
