Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
Na figura abaixo, observe os quadrados [tex]ABCD \, [/tex] e [tex] \, WXYZ[/tex] cujos lados têm comprimentos [tex]2 \, \text{cm}[/tex] e [tex] \, 1 \, \text{cm} \, [/tex], respectivamente. Observe que o lado [tex]\overline{WX}[/tex] está contido no lado [tex]\overline{DC}[/tex].
São traçadas, então, as retas definidas, respectivamente, pelos pontos [tex]D \, [/tex] e [tex] \, Z[/tex] e pelos pontos [tex]C[/tex] e [tex] \, Y[/tex], sendo que essas retas se intersectam no ponto [tex]P[/tex].
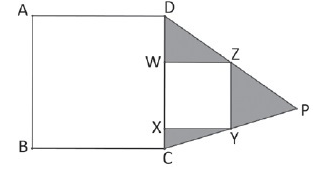
Determine a razão entre a área sombreada e a área branca do desenho.
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex].

Lembretes
(1) Teorema Fundamental da Proporcionalidade:
Se uma reta paralela a um dos lados de um triângulo intersecta os outros dois lados em pontos distintos, então ela determina um triângulo semelhante ao triângulo inicial. (Se você não se lembra dos casos de semelhança de triângulos, clique AQUI.)
(2) Em dois triângulos semelhantes, se a razão de semelhança é [tex]k[/tex], então a razão entre as alturas homólogas é [tex]k \, .[/tex]
Solução
Vamos obter separadamente a área da região branca, [tex]A_{branca} \, [/tex], e a área da região sombreada, [tex]A_{sombreada} \, .[/tex]
- Observe, inicialmente, que a área da região branca é a soma das áreas dos quadrados [tex]ABCD \, [/tex] e [tex] \, WXYZ[/tex], cujos lados sabemos que têm comprimentos [tex]2 \, \text{cm}[/tex] e [tex] \, 1 \, \text{cm}\, [/tex], respectivamente.
Assim, [tex] \, \fcolorbox{black}{#E8E8E8}{$ A_{branca}=A_{ABCD}+A_{WXYZ}=2^2+1^2=4+1=5 \, \text{cm}^2$} \, .\qquad \textcolor{#800000}{(i)}[/tex] - A área da região sombreada é a diferença entre a área [tex]A_T[/tex] do triângulo [tex]DPC \, [/tex] e a área [tex]A_Q[/tex] do quadrado [tex]WXYZ \, .[/tex]
A área do quadrado é conhecida:
[tex]\qquad A_Q=1^2=1 \, \text{cm}^2[/tex];
portanto, devemos determinar a área do triângulo [tex]DPC \, .[/tex]
Vamos lá! - A partir da figura dada no enunciado, observe que os segmentos [tex]\overline{WX} \, [/tex] e [tex] \, \overline{ZY}[/tex] são paralelos.
Assim, podemos considerar a reta definida pelos pontos [tex]Z \, [/tex] e [tex] \, Y[/tex], utilizar o Lembrete (1) e concluir que os triângulos [tex]DPC \, [/tex] e [tex] \, ZPY[/tex] são semelhantes.
E como os quadrados [tex]ABCD \, [/tex] e [tex] \, WXYZ[/tex] têm lados com comprimentos [tex]2 \, \text{cm}[/tex] e [tex] \, 1 \, \text{cm}\, [/tex], respectivamente, podemos também concluir que a razão de semelhança dos triângulos [tex]DPC \, [/tex] e [tex] \, ZPY[/tex] é [tex]\boxed{\dfrac{DC}{ZY}=\dfrac{2 \, \text{cm}}{1 \, cm}=2} \, .[/tex]
Vamos traçar a altura [tex]\overline{PR}[/tex] relativa ao lado [tex]\overline{CD}[/tex] do triângulo [tex]DPC \, [/tex] e seja [tex]S \, [/tex] o ponto de interseção dessa altura com o segmento [tex] \, \overline{ZY} \, .[/tex] Como [tex]\overline{CD} \, [/tex] e [tex] \, \overline{ZY}[/tex] são paralelos, [tex]\overline{PS} \, [/tex] é a altura do triângulo [tex]ZPY \, [/tex] relativa ao lado [tex]\overline{ZY} \, .[/tex] - pelo Lembrete (2), [tex]\dfrac{PR}{PS}=\dfrac{PD}{ZP}=2[/tex]; assim, [tex]\boxed{PR=2PS} \, , \qquad \textcolor{#800000}{(ii)}[/tex]
- por outro lado, [tex]PR=PS+SR \, [/tex] e [tex] \, SR=1[/tex]; logo, [tex]\boxed{PS=PR-1} \, , \qquad \textcolor{#800000}{(iii)}[/tex]
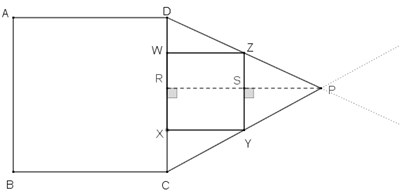
Perceba que:
assim, substituindo [tex]\textcolor{#800000}{(iii)}[/tex] em [tex]\textcolor{#800000}{(ii)}[/tex], segue que:
[tex] \qquad PR=2PS[/tex]
[tex] \qquad PR=2\left(PR-1\right)[/tex]
[tex] \qquad PR=2PR-2[/tex]
[tex] \qquad \boxed{PR=2} \, .\qquad \textcolor{#800000}{(iv)}[/tex]
Pronto, já estamos em condições de determinar a área [tex]A_T[/tex] do triângulo [tex]DPC \, [/tex]:
[tex]\qquad A_T=\dfrac{base \, \times \, altura}{2}=\dfrac{DC \times PR}{2}=\dfrac{2 \times 2}{2}=2 \, \text{cm}^2 \, .[/tex]
Com isso, a área da região sombreada já pode ser calculada:
[tex]\qquad \fcolorbox{black}{#E8E8E8}{$ A_{sombreada}=A_T-A_Q=2-1=1 \, \text{cm}^2$} \, .\qquad \textcolor{#800000}{(v)}[/tex]
Finalizando, por [tex]\textcolor{#800000}{(i)} \, [/tex] e [tex] \, \textcolor{#800000}{(v)} \, [/tex], segue que:
[tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{\text{área sombreada}}{\text{área branca}}=\dfrac{A_{sombreada}}{A_{branca}}=\dfrac{1 \, \text{cm}^2}{5 \, \text{cm}^2}=\dfrac{1}{5}$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Explorando a solução
Você observou que, na nossa solução, não consideramos a posição dos pontos [tex]W \, [/tex] e [tex] \, X[/tex] no segmento [tex]\overline{DC}[/tex]?
Veja que utilizamos nas nossas justificativas apenas o fato de o segmento [tex]\overline{WX}[/tex] estar contido no segmento [tex]\overline{DC}[/tex] e isso significa que a razão [tex]\dfrac{1}{5}[/tex] é constante, independente da posição de [tex]\overline{WX}[/tex] em [tex]\overline{DC} \, .[/tex]
Para observar geometricamente essa observação, utilize o applet abaixo.
- Movimente verticalmente o ponto [tex]\textcolor{blue}{W}[/tex] sobre o segmento [tex]\overline{DC}[/tex], observe as áreas e a razão. Veja que as áreas dos triângulos alaranjados se modificam, mas a soma total delas permanece igual a [tex]1 \, .[/tex]
Para movimentar [tex]\textcolor{blue}{W}[/tex], clique sobre ele, mantenha o mouse pressionado, e faça o movimento.
Observamos que o applet ajuda na visualização do resultado;
mas, matematicamente, não substitui sua demonstração.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
