Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Fácil)
(UFPE, 1979 -Adaptado) Uma folha de alumínio vai ser enrolada para se obter uma lata na forma de um cilindro circular reto. Em seguida, serão colocados o fundo e a tampa da lata.
Observe as imagens.

Finalizado todo o processo, determine:
-
(a) A medida do raio da base da lata.
(b) A área lateral da lata.
(c) A área total da lata.
(d) O volume da lata em [tex]ml[/tex].
Para os cálculos, utilize [tex]\pi=3,14.[/tex]
Solução
(a) Observe que ao enrolar uma folha de alumínio para obter a lata, os segmentos de comprimento [tex]314 \, mm[/tex] e destacados na figura a seguir definirão a circunferência das bases do cilindro, nas quais serão colocados o fundo e a tampa da lata.
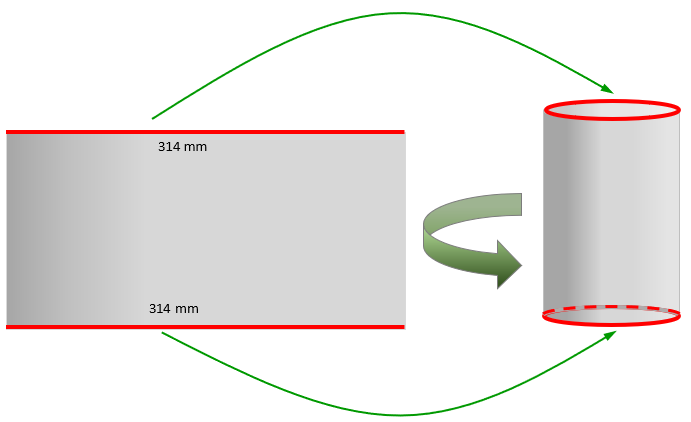
Dessa forma, o perímetro [tex]P[/tex] de cada circunferência é [tex]314 \, mm[/tex]. Assim, se denotarmos o raio da base por [tex]r[/tex], segue que:
[tex]\qquad P=314[/tex]
[tex]\qquad 2\pi r=314[/tex]
[tex]\qquad 2\times 3,14\times r=314[/tex]
[tex]\qquad r=\dfrac{314}{ 2\times 3,14}[/tex]
[tex]\quad \, r=\dfrac{314\times 100}{ 2\times 3,14 \times 100}[/tex]
[tex]\qquad r=\dfrac{\cancel{314}\times 100}{ 2\times \cancel{314}}[/tex]
[tex]\quad \, r=\dfrac{100}{2}[/tex]
[tex]\qquad r=50 \, mm \, .[/tex]
Portanto, a medida do raio da base da lata é [tex] \, \fcolorbox{black}{#eee0e5}{$50 \, mm$} \, [/tex] ou, se preferir, [tex] \, \fcolorbox{black}{#eee0e5}{$5 \, cm$} \, .[/tex]
(b) A área lateral [tex]A_{lateral}[/tex] da lata é exatamente a área da folha de alumínio que foi enrolada, ou seja:
[tex]\qquad A_{lateral}=314 \times 100[/tex]
[tex]\qquad A_{lateral}=31400 \, mm^2 \, .[/tex]

Logo, a área lateral da lata é [tex] \, \fcolorbox{black}{#eee0e5}{$31 \, 400 \, mm^2$} \, [/tex] ou ainda [tex] \, \fcolorbox{black}{#eee0e5}{$314 \, cm^2$} \, .[/tex]
(c) A área total da lata corresponde à área da região resultante da planificação da forma final da lata (com a tampa e com o fundo).
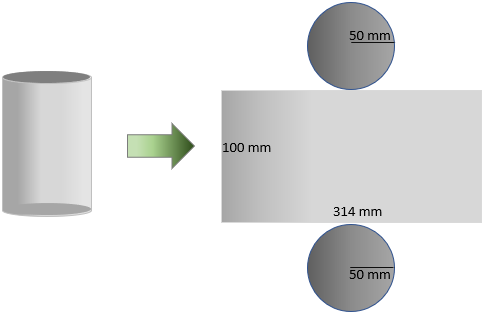
Assim, a área total da lata é a soma da área lateral com a área de dois círculos cujo comprimento [tex]r[/tex] dos raios foi calculado no item (a):
[tex]\qquad A_{total}=A_{lateral}+2\times \left(\pi r^2 \right)[/tex]
[tex]\qquad A_{total}=31400+2 \times 3,14 \times \left(50\right)^2[/tex]
[tex]\qquad A_{total}=31400+15700[/tex]
[tex]\qquad A_{total}=47100 \, mm^2 \, . [/tex]
Dessa forma, a área total da lata é [tex] \, \fcolorbox{black}{#eee0e5}{$47\,100 \, mm^2$} \, [/tex] ou [tex] \, \fcolorbox{black}{#eee0e5}{$471 \, cm^2$} \, .[/tex]
(d) O volume da lata é o volume de um cilindro circular reto, logo é dado pelo produto entre a área da base e a altura da lata em questão, sendo que a área da base é a área do círculo de raio [tex]r=50 \, mm \, .[/tex]
Como as medidas foram dadas em milímetros, vamos inicialmente calcular o volume [tex]V[/tex] da lata em [tex]mm^3[/tex]; vejamos:
[tex]\qquad V=\text{área da base} \times \text{altura}[/tex]
[tex]\qquad V= \left(\pi r^2 \right)\times100[/tex]
[tex]\qquad V=785000 \, mm^3 \, .[/tex]
- Sabemos que [tex]\boxed{1 \, ml=1 \, cm^3} \, [/tex]; logo, vamos transformar o volume de [tex]mm^3[/tex] para [tex]cm^3 \, .[/tex] Mas, para isso, devemos lembrar que [tex]\boxed{1 \, cm^3=1000 \, mm^3}[/tex] ou, de outra forma, [tex]\boxed{1 \, mm^3=0,001 \, cm^3} \, .[/tex]
Consequentemente,
[tex]\qquad V=785000 \, mm^3= \, 785000 \times 0,001 \, cm^3= 785 \, cm^3 \, .[/tex]
Finalizando, o volume solicitado neste item é [tex] \, \fcolorbox{black}{#eee0e5}{$785 \, ml$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
