Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir do 1º ano do E. M.)
- Existe uma lei da Física que garante que a intensidade luminosa [tex]I_F[/tex], medida em candela, que uma fonte luminosa [tex]F[/tex] produz sobre um ponto [tex]Q[/tex], situado a uma distância [tex]d[/tex] de [tex]F[/tex], é diretamente proporcional à potência luminosa [tex]P[/tex] da fonte e inversamente proporcional ao quadrado da distância [tex]d[/tex].
Considere duas fontes luminosas, situadas a uma distância de [tex]10[/tex] metros uma da outra, tais que a potência de uma é quatro vezes maior que a potência da outra.
Se [tex]A[/tex] e [tex]B[/tex] são pontos que representam as duas fontes, sendo [tex]A[/tex] o ponto que representa a fonte de maior potência, determine os pontos da reta por eles definida que sejam igualmente iluminados pelas duas fontes.
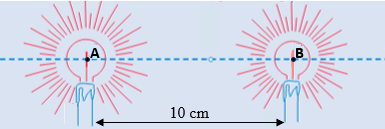
Adaptado de Álgebra – Aurélio Baldor.
Solução
Sem perda de generalidade, vamos escolher o ponto [tex]A[/tex] como origem de um eixo orientado [tex]Ax[/tex] cuja orientação positiva vai de [tex]A[/tex] para [tex]B[/tex].

Seja [tex]C[/tex] um ponto da reta definida pelos pontos [tex]A[/tex] e [tex]B[/tex] igualmente iluminado pelas duas fontes e seja [tex]x[/tex] a sua coordenada. Desta maneira, a distância entre [tex]A[/tex] e [tex]C[/tex] será [tex]|x|[/tex] e a distância entre [tex]B[/tex] e [tex]C[/tex] será [tex]|10-x|[/tex].
Assim, pelo princípio da Física enunciado acima, a intensidade luminosa da fonte [tex]A[/tex] sobre [tex]C[/tex] será
[tex]\quad I_A=\mu \dfrac{4P}{|x|^2}[/tex]
e a intensidade luminosa da fonte [tex]B[/tex] sobre [tex]C[/tex] será
[tex]\quad I_B=\mu\dfrac{P}{|10-x|^2},[/tex]
para alguma constante positiva [tex]\mu[/tex].
Procuramos pelos valores de [tex]x[/tex] tais que [tex]I_A=I_B[/tex]; assim, como [tex] |x|^2=x^2[/tex] e [tex]|10-x|^2=(10-x)^2[/tex], temos que
[tex]\quad \dfrac{4P}{x^2}=\dfrac{P}{(10-x)^2}.[/tex]
Vamos, então, resolver a equação [tex]4P(10-x)^2=Px^2.[/tex]
- Como a potência é não nula podemos dividir ambos os membros por [tex]P[/tex], obtendo a seguinte sequência de igualdades:
[tex]\qquad 4(10-x)^2=x^2[/tex]
[tex]\qquad 4(100-20x+x^2)=x^2[/tex]
[tex]\qquad 400-80x+4x^2=x^2[/tex]
[tex]\qquad \boxed{3x^2-80x+400=0}.[/tex]
Estamos com uma equação do segundo grau cujo discriminante é dado por
[tex]\qquad \Delta=80^2-4\cdot 3 \cdot 400\\
\qquad \Delta=6400-4800=1600=40^2,[/tex]
logo, as raízes são:
[tex]\quad x_1=\dfrac{80-40}{6}=\dfrac{20}{3}=6,666\cdots[/tex]
[tex]\quad x_2=\dfrac{80+40}{6}=\dfrac{120}{6}=20.[/tex]
Assim, existem dois pontos na reta [tex]AB[/tex] que são igualmente iluminados pelas fontes em [tex]A[/tex] e [tex]B[/tex]: um deles se encontra entre [tex]A[/tex] e [tex]B[/tex], aproximadamente [tex]6,7\text{ m}[/tex] distante de [tex]A[/tex], e o outro se encontra à direita de [tex]A[/tex] e de [tex]B[/tex], a [tex]20\text{ m}[/tex] de [tex]A[/tex].

Solução elaborada pelos Moderadores do Blog.
