Problema
(Indicado a partir do 6º ano do E. F.)
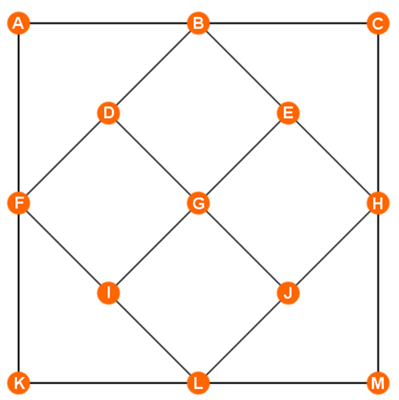
Na figura abaixo há treze círculos ligados por 10 linhas, cada uma delas com três círculos. Escolha treze números inteiros, sendo doze diferentes, e substitua as letras por esses números de modo que a soma dos números de cada linha seja 20.
Dica: Use números de 1 a 15.
Solução 1
Partindo do conceito de que a soma de dois números pares é sempre par, e a de dois números ímpares também é sempre par, notamos que o número do centro do cristal deve ser um número par.
Assim sendo, chegamos a conclusão que D e J ; I e E poderiam ser duplas de números pares, que somados ao número central resultariam também em um número par, ou seja, o 20.
Usamos então como número central o 4 , para D = 14 , J = 2 ; E = 12 , I = 4.
Partindo disso temos que B = 1 , F = 5 , H = 7 , L = 11.
E por fim , A = 9 , C = 10 , K = 6 , M = 3.
Observação: Chegamos a resposta sem usar os números 8 , 13 e 15.
Solução elaborada pelo Clube AS PRIMAS E EU.
Solução 2
Nós começamos a pensar qual poderia ser o número centro e chegamos no número 2, aí conseguimos fechar nas 10 linhas o resultado 20, sendo agora A=5; B=10; C=5; D=3; E=6; F=7; G=2; H=4; I=12; J=15; K=8; L=1; M=11.
Solução elaborada pelo Clube Mini-einstein’s.
Solução 3
- A =7; B= 10; C= 3;
- D=5; E= 4;
- F= 5; G= 2; H= 6;
- I= 14; J= 13;
- K= 8; L= 1; M= 11.
Solução elaborada pelo Clube MIRIM APRENDIZ.
