Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
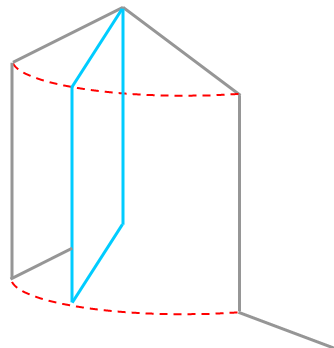
Uma porta giratória medindo [tex]2,0 \, m[/tex] de altura por [tex]76 \, cm[/tex] de largura gira um quarto de volta em torno de suas dobradiças.
Qual o volume do sólido descrito por ela? Expresse o resultado em metros cúbicos e em centímetros cúbicos.
Solução
Perceba que o sólido descrito pela rotação da porta depois de ela girar um quarto de volta corresponde a um quarto de um cilindro circular reto de raio [tex]76 \, cm[/tex] e com [tex]2,0 \, m[/tex] de altura, conforme você pode observar na figura abaixo.
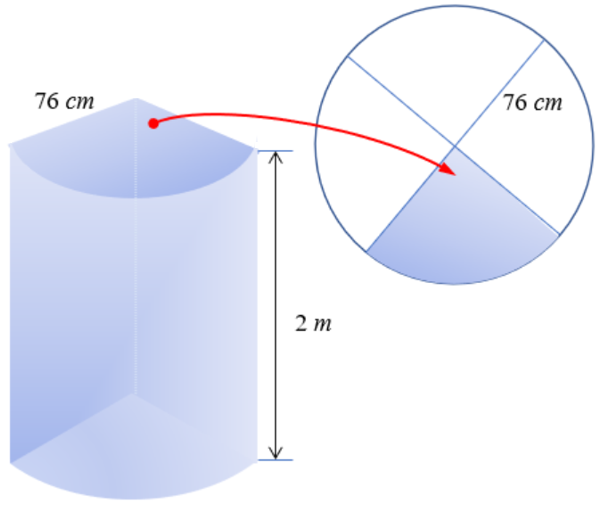
O volume de um cilindro circular reto de raio [tex]r[/tex] e altura [tex]h[/tex] é dado por
[tex]\qquad V_c=\text{área da base}\times \text{altura}=\left(\pi \, r^2\right)\times h \, [/tex],
e como o resultado deve ser expresso em metros cúbicos e em centímetros cúbicos, podemos fazer os cálculos em centímetros cúbicos e transformar o resultado para metros cúbicos ou fazer os cálculos em metros cúbicos e transformar para centímetros cúbicos. Faremos das duas maneiras.
| O volume [tex]V[/tex] do sólido descrito pela rotação da porta, em [tex]cm^3[/tex] pode ser assim calculado: [tex]\qquad V=\dfrac{\left(\pi \, r^2\right)\times h}{4} \, [/tex]
[tex]\qquad V=\dfrac{\left(\pi\times \, 76^2\right)\times \cancel{200}}{\cancel{4}} \, [/tex] |
O volume [tex]V[/tex] do sólido descrito pela rotação da porta, em [tex]m^3[/tex] pode ser assim calculado: [tex]\qquad V=\dfrac{\left(\pi \, r^2\right)\times h}{4} \, [/tex]
[tex]\qquad V=\dfrac{\left(\pi\times \, 0,76^2\right)\times 2}{4} \, [/tex]
[tex]\qquad V= 0,1444\times \pi\times 2 \, [/tex] |
Portanto, o volume correspondente ao sólido descrito pela rotação da porta ao girar um quarto de volta é igual a
[tex]\qquad \qquad \fcolorbox{black}{#eee0e5}{$288\,800\,\pi \, cm^3$}\qquad [/tex] ou [tex]\qquad \fcolorbox{black}{#eee0e5}{$0,2888\,\pi \, m^3$} \, [/tex],
e, aproximadamente,
[tex]\qquad \qquad \fcolorbox{black}{#eee0e5}{$906\,832 \, \,cm^3$}\qquad [/tex] ou [tex]\qquad \fcolorbox{black}{#eee0e5}{$ 0,91 \, m^3$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
