Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
A figura abaixo é formada por quatro semicírculos.
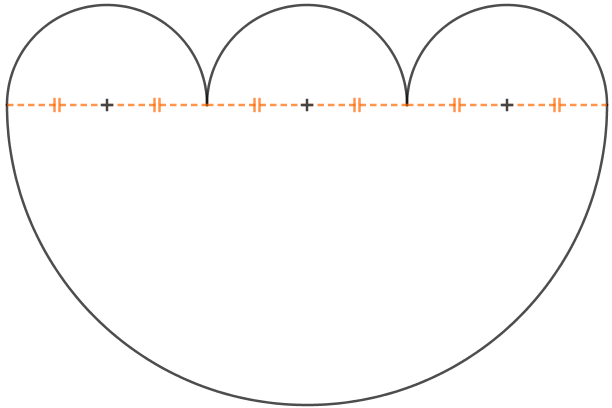
Sendo [tex]1,4 \, cm[/tex] o comprimento do raio de cada um dos três semicírculos menores, determine:
(a) Uma aproximação, com duas casas decimais, do valor em centímetros do perímetro da figura.
(b) Uma aproximação, com duas casas decimais, do valor em centímetros quadrados da área da figura.
Para os cálculos, utilize [tex]\pi=3,14.[/tex]
Solução
Observe inicialmente que o raio [tex]R[/tex] do semicírculo maior corresponde a três raios de um semicírculo menor, ou seja:
[tex]\qquad R=3 \times 1,4 \, cm=4,2 \, cm[/tex].
(a) O perímetro [tex]P[/tex] da patinha é dado pela soma de quatro semiperímetros de círculos: três de raio [tex]1,4 \, cm[/tex] e um de raio [tex]4,2 \, cm[/tex]:
[tex]\qquad P=3\times \dfrac{\cancel{2}\times \pi \times 1,4}{\cancel{2}}+\dfrac{\cancel{2}\times \pi \times 4,2}{\cancel{2}}[/tex]
[tex]\qquad P=\pi \times \left(3\times 1,4+4,2\right)[/tex]
[tex]\qquad P=\pi \times 8,4[/tex]
[tex]\qquad P= 3,14 \times 8,4[/tex]
[tex]\qquad P= 26,376[/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$P\approx 26,38 \, cm$} \, .[/tex]
![]()
(b) De maneira análoga, a área [tex]A[/tex] da patinha é dada pela soma das áreas de quatro semicírculos: três de raio [tex]1,4 \, cm[/tex] e um de raio [tex]4,2 \, cm. \, [/tex]
Assim:
[tex]\qquad A=3\times \dfrac{\pi \times \left(1,4\right)^2}{2}+\dfrac{\pi \times \left(4,2\right)^2}{2}[/tex]
[tex]\qquad A=\dfrac{\pi}{2} \times \left(3\times \left(1,4\right)^2+\left(4,2\right)^2\right)[/tex]
[tex]\qquad A=\dfrac{\pi}{2} \times \left(3\times 1,96+17,64\right)[/tex]
[tex]\qquad A=\dfrac{\pi}{2} \times \left(5,88+17,64\right)[/tex]
[tex]\qquad A=\dfrac{\pi}{2} \times 23,52[/tex]
[tex]\qquad A=\dfrac{3,14}{2} \times 23,52[/tex]
[tex]\qquad A=1,57 \times 23,52[/tex]
[tex]\qquad A=36,9264[/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$A\approx 36,93 \, cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
