Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
Prolongando-se os lados de um pentágono regular, construímos uma estrela.
Determine, em graus, as medidas [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] dos ângulos destacados na figura.
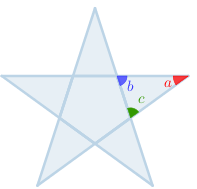

Lembretes
✐ A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex].
✐ A medida de cada ângulo interno de um pentágono regular é [tex]108^{\circ}[/tex]. (Se você não sabe como justificar esse resultado, clique AQUI).
Solução
Observe a figura abaixo.
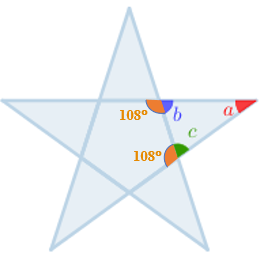
Como a medida de cada ângulo interno de um pentágono regular é [tex]108^{\circ}[/tex], então
- [tex]b+108^{\circ}=180^{\circ}[/tex]
- [tex]c+108^{\circ}=180^{\circ}.[/tex]
Assim, concluímos facilmente que [tex]b=c=180^{\circ}-108^{\circ}=72^\circ[/tex].
Por outro lado, a soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex], logo:
[tex]\qquad a+b+c=180^{\circ}[/tex]
[tex]\qquad a+72^\circ+72^\circ=180^{\circ}[/tex]
[tex]\qquad a+144^\circ=180^{\circ}[/tex]
[tex]\qquad a=180^{\circ}-144^\circ[/tex]
[tex]\qquad a=36^\circ.[/tex]
Pelo exposto, [tex] \, \fcolorbox{black}{#eee0e5}{$a=36^\circ$} \, [/tex], [tex] \, \fcolorbox{black}{#eee0e5}{$b=72^\circ$} \, [/tex] e [tex] \, \fcolorbox{black}{#eee0e5}{$c=72^\circ$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
