Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
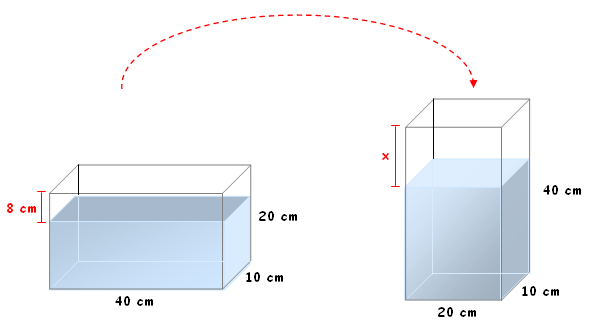
Um bloco de vidro na forma retangular, com dimensões [tex]40 cm \, \times \, 10 cm \, \times \, 20 cm[/tex], totalmente fechado e com água dentro, foi colocado em pé. (Veja a figura abaixo.)
Na nova posição, determine a distância x.

Lembrete
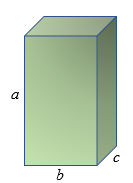
✐ O volume de um bloco retangular (ou paralelepípedo retorretângulo) cujos lados expressos na mesma unidade de comprimento medem [tex]a \, ; \, b \, ; \, c \, [/tex] é o produto dessas três medidas:
[tex]\qquad \qquad \boxed{V=a \cdot b \cdot c} \, .[/tex]
Solução
Observe que, embora o bloco de vidro comporte um volume
- [tex]V_{total}=40\times 10 \times 20=8000 \, cm^3[/tex] de água,
dentro dele há apenas
- [tex]V_{\text{água}}40\times 10 \times (20-8)=40\times 10 \times 12=4800 \, cm^3[/tex] de água.
Perceba que, ao mudarmos o bloco de vidro de posição, o volume de água permanece o mesmo: [tex] \boxed{V_{\text{água}}=4800 \, cm^3} \, [/tex].
Na posição em pé, podemos considerar que o bloco retangular de vidro é formado por dois blocos retangulares menores: um definido pelo volume de água dentro dele e outro, de altura [tex]x[/tex], que corresponde à parte vazia dele, conforme mostra a próxima figura.
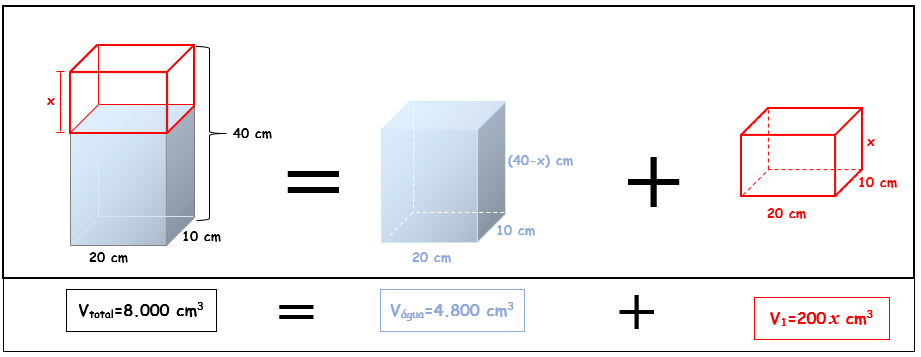
Dessa forma, podemos calcular a distância [tex]x[/tex] de dois modos; observe.
- Observe que, na posição em pé, o volume de água [tex] \boxed{V_{\text{água}}=4800 \, cm^3} \, [/tex] ocupa um bloco retangular cujas dimensões em centímetros são: [tex]20 \, ; \, 10 \, ; \, 40-x[/tex].
Assim:
[tex]\qquad 4800 \, cm^3=20\times 10 \times (40-x)cm^3[/tex]
[tex] \qquad 4800=200(40-x)[/tex]
[tex] \qquad 48=2(40-x)[/tex]
[tex] \qquad 24=40-x[/tex]
[tex] \qquad x=40-24[/tex]
[tex] \qquad \boxed{x=16} \, .[/tex] - Observe que, na posição em pé, o volume do bloco retangular vazio é a diferença entre o volume total do bloco de vidro e o volume d’água.
Como o bloco retangular vazio tem dimensões em centímetros iguais a [tex]20 \, ; \, 10 \, ; \, x \, [/tex], segue que:
[tex]\qquad 8000-4800=20\times 10 \times x[/tex]
[tex]\qquad 3200=200x[/tex]
[tex]\qquad 32=2x[/tex]
[tex] \qquad \boxed{x=16} \, .[/tex]
De qualquer forma, temos que [tex] \, \fcolorbox{black}{#eee0e5}{$x=16 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
