Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil)
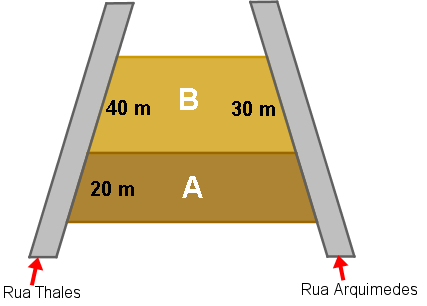
André e Benê compraram respectivamente os terrenos A e B, na forma de trapézio, mostrados na figura abaixo.
Na frente de ambos fica a rua Arquimedes e, no fundo, a rua Thales.
Quantos metros tem a frente do terreno de André?

Ajuda
Para solucionar este problema será necessário utilizarmos um importantíssimo resultado da Geometria Plana atribuído a Tales de Mileto!
Teorema de Tales: Se um feixe de retas paralelas, com no mínimo três retas, é intersectado por duas transversais, os segmentos de reta produzidos pelas paralelas sobre as transversais são proporcionais.
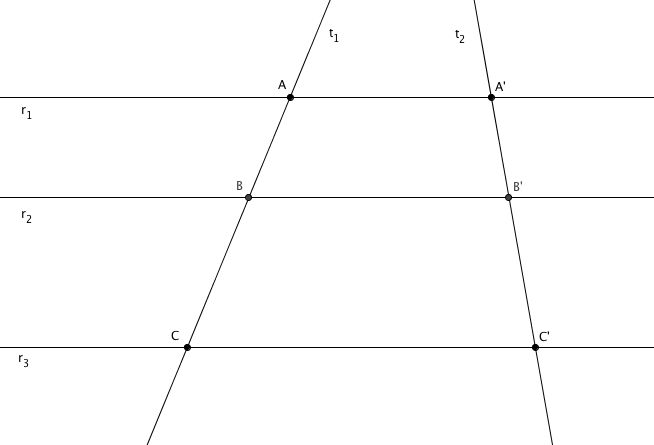
Se [tex]r_1[/tex], [tex]r_2[/tex] e [tex]r_3[/tex] são retas paralelas e [tex]t_1[/tex] e [tex]t_2[/tex] são retas transversais a [tex]r_1[/tex], [tex]r_2[/tex] e [tex]r_3[/tex], conforme mostra a figura a seguir, então
[tex]\qquad \qquad \dfrac{AB}{A’B’} = \dfrac{BC}{B’C’}[/tex]
sendo que [tex]AB, \, BC, \, A’B’, \, B’C'[/tex] denotam, respectivamente, os comprimentos dos segmentos [tex]\overline{AB}, \, \overline{BC}, \, \overline{A’B’}, \, \overline{B’C’}[/tex].
Solução
Seja [tex]x[/tex] o comprimento em metros da frente do terreno A.
Simplificando o desenho dado no problema, percebemos que estamos em condições de aplicarmos o teorema de Tales, visto que, tendo os terrenos forma de trapézios, os segmentos horizontais são paralelos.
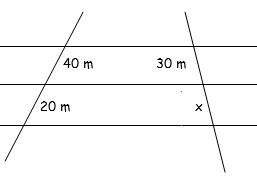
Assim, segue que:
[tex]\qquad \dfrac{40}{30}=\dfrac{20}{x}[/tex]
[tex]\qquad 40x=30 \times 20[/tex]
[tex]\qquad 40x=600[/tex]
[tex]\qquad x=\dfrac{600}{40}[/tex]
[tex]\qquad x=15.[/tex]
Portanto, a frente do terreno de André mede [tex] \, \fcolorbox{black}{#eee0e5}{$15 \, m$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
