Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Médio)
Seis tubos cilíndricos com [tex]10[/tex] cm de raio cada um e feitos com material não deformável foram empilhados. A figura abaixo mostra uma vista de frente dos cilindros.
Determine a altura aproximada da pilha, em metros, utilizando uma casa decimal.
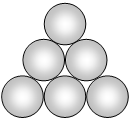
Observação: Para efeito dos cálculos, despreze a espessura das paredes dos tubos.

Ajuda
Observem a figura a seguir e percebam que a altura da pilha de tubos não é a soma dos diâmetros de três tubos ou, de maneira equivalente, não é a soma de seis raios.
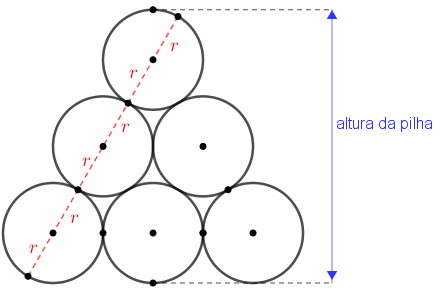
Solução
Seja [tex]r[/tex] a medida em centímetros dos raios dos tubos empilhados.
A figura abaixo nos mostra que se [tex]h[/tex] é o segundo cateto de um triângulo retângulo com um cateto e a hipotenusa com comprimentos [tex]2r\, [/tex] e [tex]\, 4r\, [/tex], respectivamente, então a altura da pilha será [tex]\, \boxed{A_p=h+2r}\, .[/tex]
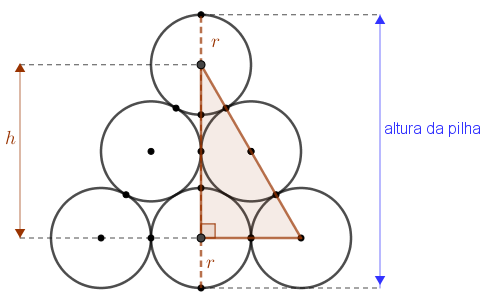
Vamos então calcular [tex]h\, [/tex].
- Pelo teorema de Pitágoras, segue que:
[tex]\qquad h^2+\left(2r\right)^2=\left(4r\right)^2[/tex]
[tex]\qquad h^2+4r^2=16r^2[/tex]
[tex]\qquad h^2=12r^2.[/tex]
Como [tex]h \gt 0[/tex], pois é um comprimento, e [tex]r=10\gt 0[/tex] temos que
[tex]\qquad h=\sqrt{12}r[/tex]
[tex]\qquad h=10\sqrt{12}\, cm.[/tex]
Portanto,
[tex]\qquad A_p=h+2r[/tex]
[tex]\qquad A_p=10\sqrt{12}+2\times 10[/tex]
[tex]\qquad A_p=10\sqrt{12}+20[/tex]
[tex]\qquad A_p\approx 54,64\, cm[/tex]
[tex]\qquad A_p\approx 0,5464\, m.[/tex]
Assim, a altura aproximada da pilha em metros e com uma casa decimal é [tex]\, \fcolorbox{black}{#eee0e5}{$0,5$}\, [/tex], ou seja, [tex]\, \fcolorbox{black}{#eee0e5}{$\text{meio metro}$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
