Problema
(Indicado a partir do 6º ano do E. F.)
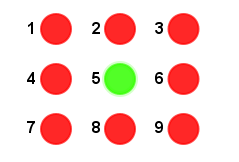
Um jogo utiliza um painel com 9 botões luminosos, posicionados conforme indica figura abaixo.

Quando apertados, esses botões alternam entre a cor vermelha e a verde da seguinte forma:
- apertando um botão da borda do retângulo, trocam de cor ele e seus vizinhos (do lado e na diagonal).
- apertando o botão do centro, trocam de cor todos os seus 8 vizinhos, porém ele não.
Por exemplo,
– apertando o botão 1, mudam de cor os botões 1, 2, 4 e 5.
– apertando o botão 2, mudam de cor os botões 1, 2, 3, 4, 5 e 6.
Inicialmente todos os botões estão verdes.

É possível, apertando sucessivamente alguns botões, torná-los todos vermelhos?
(Adaptado da Edição Especial da Revista Eureka – 2007.)
Solução
Observe que:
- Apertando um dos botões do canto (1, 3, 7 ou 9), alteramos a cor de 4 luzes, restando 5 com a cor inalterada.
- Apertando um dos botões dos lados (2, 4, 6 ou 8), alteramos a cor de 6 luzes, restando 3 com a cor inalterada.
- Apertando o botão do meio, alteramos a cor de 8 luzes, restando uma com a cor inalterada.
Note que as cores das luzes sempre se alteram numa quantidade PAR e temos um total ÍMPAR de luzes; então não é possível tornar todos os botões vermelhos, pois sempre restará pelo menos um com a cor verde (cor inicial).
Solução elaborada pelo COM Fernandes Lima Alagoas, com colaboração dos Moderadores do Blog.
AJUDA
 |
Se você se atrapalhou com a argumentação da paridade das cores, talvez as figuras abaixo possam ajudar!
|
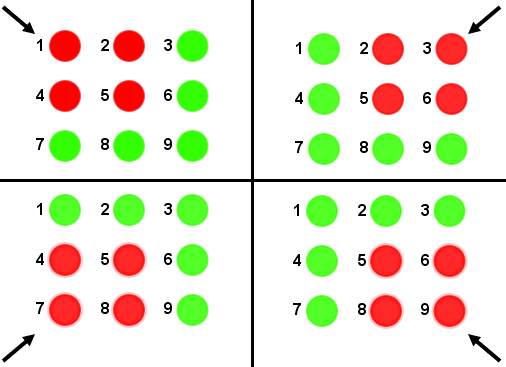
- Por exemplo, as quatro imagens abaixo ilustram, respetivamente, as situações obtidas ao clicarmos nos botões 1, 3, 7 ou 9, a partir da situação inicial do painel.
- As próximas imagens ilustram, respetivamente, as situações obtidas ao clicarmos nos botões 2, 4, 6 ou 8, a partir da situação inicial do painel.
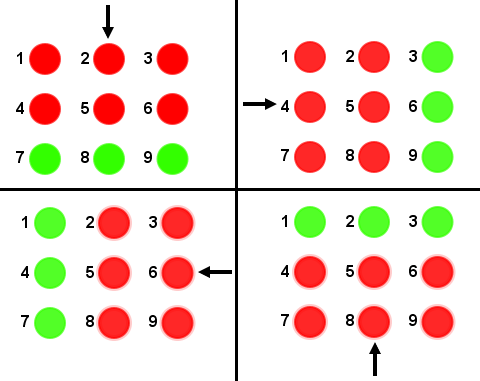
- A última imagem ilustra a situação obtida ao clicarmos no botão 5, a partir da situação inicial do painel.