Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir do 8º ano do E. F.)
Um hexágono regular de lado [tex]x[/tex] foi dividido em duas partes por segmentos internos que medem [tex]1, 2, 3, 4, 5[/tex] e [tex]6[/tex] unidades de comprimento. Dois segmentos adjacentes são perpendiculares como mostra a figura.
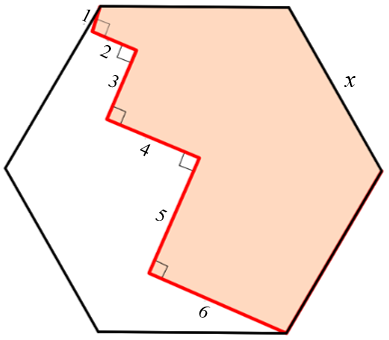
Determine o perímetro da região colorida.
Extraído do Twitter.
AJUDA
Todo hexágono regular pode ser dividido em seis triângulos equiláteros iguais cujos lados são iguais ao lado do hexágono.
OBMEP_srg, criado com o GeoGebra
Solução
O perímetro da região colorida é dado por
[tex]\quad P=1+2+3+4+5+6+x+x+x\\
\quad P=21+3x.[/tex]
Portanto, precisamos determinar o valor de [tex]x.[/tex]
Para isso, note que, como os segmentos internos adjacentes são perpendiculares, podemos construir o triângulo retângulo de catetos [tex]1+3+5=9~[/tex] e [tex]~2+4+6=12[/tex] destacado em azul na imagem abaixo.
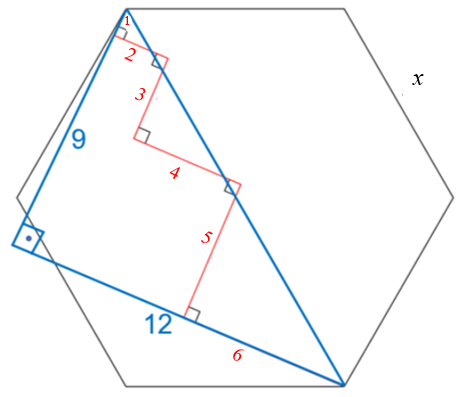
Por outro lado, como o hexágono é regular, a hipotenusa do triângulo azul corresponde à junção de dois lados do hexágono. De fato, de acordo com a ajuda, o hexágono pode ser dividido em seis triângulos equiláteros iguais cujos lados são iguais aos seus lados. Dessa forma, hipotenusa tem comprimento [tex]2x[/tex].
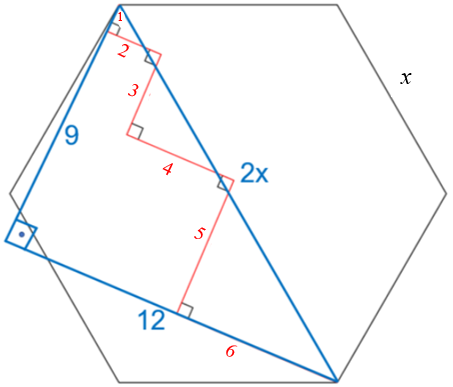
Aplicando o Teorema de Pitágoras no triângulo em questão, obtemos:
[tex]\quad (2x)^2=9^2+12^2\\
\quad(2x)^2=81+144\\
\quad (2x)^2=225\\
\quad 2x=15\\
\quad x=7,5.[/tex]
Logo, o perímetro pedido é igual a
[tex]\quad P=21+3x=21+3\cdot 7,5[/tex]
[tex] \quad \boxed{P=43,5}[/tex] unidades de comprimento.
Solução elaborada pelos Moderadores do Blog.
