Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir do 2º ano do E. F.)
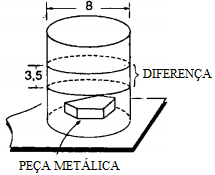
Um cilindro circular reto possui água até a metade de sua capacidade total.
Uma peça metálica é jogada no interior desse cilindro e, com isso, o nível da água sobe [tex]3,5 \text{ cm}[/tex].
Se o diâmetro do cilindro for de [tex]8\text{ cm}[/tex], qual é o volume da peça?
Extraído de Geometría – Teoría y Práctica.
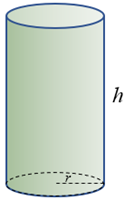
Lembrete
✐ Volume de um cilindro circular reto cujo comprimento da altura é [tex]h[/tex] e o comprimento do raio da base é [tex]r[/tex]:
[tex]\qquad \qquad \boxed{Volume=\pi\,r^2 h}.[/tex]
Solução
A diferença de altura da água antes e depois de a peça metálica ser jogada dentro do cilindro se deve ao volume dessa peça.
Assim, o volume da peça metálica corresponde exatamente ao aumento do volume ocupado pela água após a peça ser jogada dentro do cilindro.
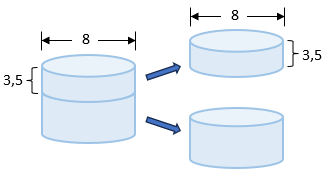
Portanto, o volume [tex]V[/tex] da peça metálica é dado por:
[tex]\qquad V= \pi r^2h=\pi\cdot 4^2\cdot 3,5\\
\qquad \boxed{V=56\pi\approx 175,84 \text{ cm}^3}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Participaram da discussão os Clubes: FIBONACCI ; Geomestres Slay ; Obmépicos; Os Somados ; Potências de Euler ; União Fibonacci .
