Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir do 9º ano do E. F.)
Conta uma lenda que Pitágoras (569 a.C. – 480 a.C., aproximadamente) despertou sua curiosidade em relação à música quando, ao passar em frente à oficina de um ferreiro, ouviu o som de cinco martelos batendo em uma bigorna e percebeu que os martelos soavam harmonicamente, exceto um. Curioso, ele tentou estabelecer uma relação entre os martelos que eram harmônicos e, para pesquisar os sons correspondentes às relações que observou, Pitágoras construiu um monocórdio: uma caixa de ressonância sobre a qual era estendida uma única corda presa a dois cavaletes.
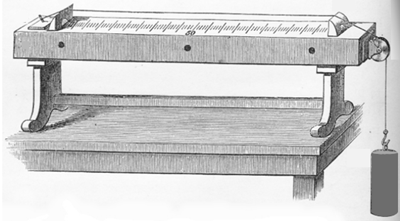 Imagem adaptada de Laboratório de Luthieria. (Acesso em 07/12/23)
Imagem adaptada de Laboratório de Luthieria. (Acesso em 07/12/23)
A partir de divisões feitas na corda, ele observou que o som produzido pressionando metade da corda era o mesmo, porém mais agudo, que o som produzido pela corda inteira: ou seja, pressionando a corda na metade, se produzia o som no que chamamos de “uma oitava acima”.
Hoje, sabemos que o som é uma onda, e cada nota é dada por uma onda que oscila com certa frequência. O hertz (símbolo Hz) é a unidade do Sistema Internacional (SI) para medida de frequências e expressa, em termos de ciclos por segundo, a frequência de um evento periódico. Assim, se uma onda sonora completar 100 oscilações em 1 segundo, por exemplo, sua frequência será de 100 Hz.
Então, a experiência de Pitágoras significa que, quando uma frequência é multiplicada por 2, a nota permanece a mesma. Por exemplo, a frequência da nota Lá (440 Hz) multiplicada por 2 é também uma nota Lá (880 Hz), só que uma oitava acima (um Lá mais agudo).
Na música ocidental, em uma oitava (por exemplo, entre duas notas Dó consecutivas), há 12 intervalos chamados de semitons.
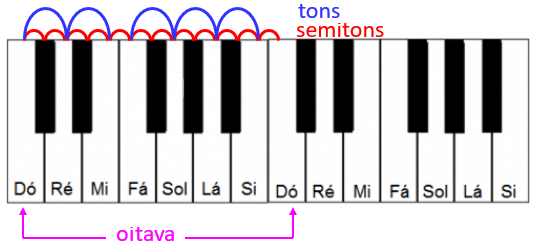
As frequências de duas notas consecutivas (isto é, cuja distância é de 1 semitom) se relacionam da seguinte forma: a frequência da segunda é a frequência da primeira multiplicada por uma constante [tex]c[/tex].
Qual o valor de [tex]c[/tex]?
Solução
Suponha que uma nota, por exemplo, um Dó, tenha frequência [tex]x[/tex]; a frequência da próxima nota (da esquerda para a direita) será então [tex]xc[/tex], a próxima nota terá frequência [tex]xc^2[/tex], a próxima, [tex]xc^3[/tex] e assim por diante, até a frequência [tex]xc^{12}[/tex], que ocupa a 13ª tecla.
Como há 12 intervalos de semitons entre essas notas, a 13ª nota também será Dó: uma oitava acima da nota Dó anterior (mais grave). Dessa forma, como a frequência é dobrada em uma oitava, a 13ª nota terá frequência igual a [tex]2x[/tex]. Temos então que:
[tex]\qquad xc^{12} = 2x\\
\qquad c^{12} = \dfrac{2x}{x}\\
\qquad c^{12} =2\\
\qquad c = \sqrt[12]{2}\\
\qquad \boxed{c\approx 1,059}.[/tex]
Solução elaborada pelo COM União Fibonacci, com contribuições dos Moderadores do Blog.
