Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir do 7º ano do E. F.)
Cinco retângulos congruentes foram desenhados de forma a obtermos um retângulo maior, conforme mostra a figura.
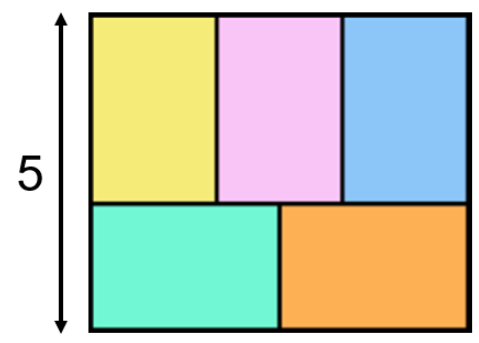
Qual a área do retângulo maior?
Extraído de Twitter.
Solução
Sejam [tex]~m~[/tex] e [tex]~5-m[/tex] as medidas das dimensões de cada retângulo. Observe a figura abaixo.
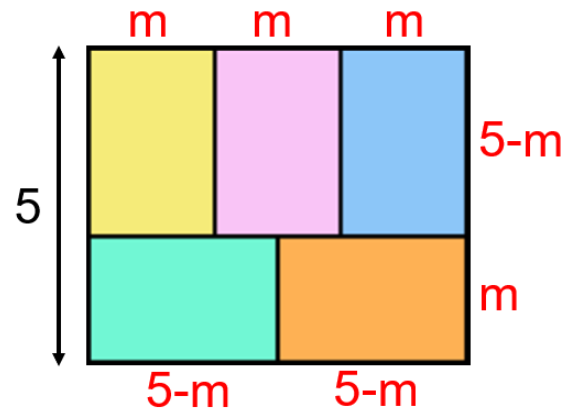
A partir daí, podemos escrever:
[tex]\qquad 3 \cdot m=2 \cdot (5-m)\\
\qquad3 \cdot m=10-2 \cdot m\\
\qquad 5 \cdot m=10\\
\qquad m=2.[/tex]
Desta forma, a área do retângulo maior é dada por:
[tex]\qquad 5 \cdot (3 \cdot m)=30[/tex] unidades de área.
Solução elaborada pelos Moderadores do Blog.
Participaram da discussão os Clubes: Puzzlers [tex]\pi[/tex]rados ; Numeradores ; Geomestres Slay ; Potências de Euler ; Phidias ; Exponenciais ; Os Últimos Alunos de Fermat ; Obmépicos ; Amigoritmos ; Super Gênios [tex]3^\circ[/tex] CPM ; Fibonacci ; União Fibonacci ; Lapidando Vencedores Matemáticos.
