✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 1º ano do E. M.)
Na figura a seguir, visualizamos duas placas triangulares regulares (triângulos equiláteros) [tex]ABC[/tex] e [tex]A’B’C'[/tex] que possuem o mesmo baricentro [tex]G[/tex] e tais que [tex]\overline{AB}//\overline{A’B’}[/tex], [tex]\overline{AC}//\overline{A’C’}[/tex] e [tex]\overline{BC}//\overline{B’C’}.[/tex]
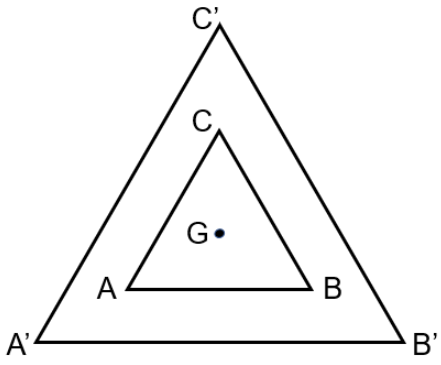
Se a medida dos lados de [tex]ABC[/tex] é igual a [tex]3 \cdot \sqrt{3}[/tex] cm e a distância entre os lados paralelos mede [tex]2[/tex] cm, qual a medida das alturas da placa [tex]A’B’C'[/tex]?

Lembretes e notações
(1) Em um triângulo equilátero de lado [tex]l[/tex], qualquer uma das três alturas mede [tex]\dfrac{l\sqrt{3}}{2}[/tex].
(2) Em um triângulo equilátero, o baricentro (que também é incentro, circuncentro e ortocentro) divide os segmentos relativos às alturas (que também são medianas, mediatrizes e bissetrizes) numa razão de [tex]2[/tex] para [tex]1[/tex].
Notações: Denotaremos o segmento definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e o seu comprimento por [tex]XY[/tex].
Solução
Seja [tex]\overline{CM}[/tex] a altura, a mediana e a bissetriz relativas ao vértice [tex]C[/tex] no triângulo [tex]ABC.[/tex]
Como [tex]G[/tex] é baricentro de [tex]ABC[/tex], então [tex]GM = x[/tex] faz com que [tex]CG = 2x[/tex].
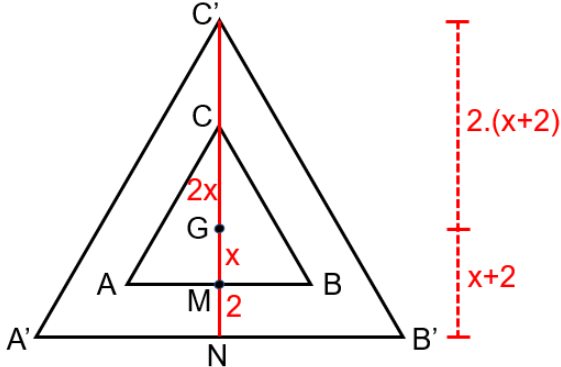
Assim, como [tex]MN = 2[/tex], temos que [tex]GN = x+2~[/tex] e [tex]~C’G = 2 \cdot (x+2) [/tex].
Agora, como [tex]\overline{CM}[/tex] é altura do triângulo equilátero [tex]ABC[/tex] de lado [tex]l = 3 \cdot \sqrt{3}[/tex], então
[tex]\qquad CM=3x=\dfrac{l \sqrt{3}}{2}=\dfrac{3 \cdot \sqrt{3} \cdot \sqrt{3}}{2}=\dfrac{9}{2}=4,5[/tex],
donde
[tex]\qquad x=1,5[/tex] cm.
Finalmente podemos calcular a altura da placa triangular [tex]A’B’C’[/tex]:
[tex]\qquad x+2+2 \cdot (x+2)=3x+6=3 \cdot 1,5 +6 = \boxed{10,5 \text{ cm}}.[/tex]
Solução elaborada pelos Moderadores do Blog.
