Clique no botão abaixo para visualizar a Sala.
Nesta Sala vamos fazer alguns exemplos mais envolvendo composição de funções.
[tex]\qquad \begin{eqnarray*}
f:\mathbb{R} &\rightarrow & \mathbb{R}\qquad \qquad g:& \mathbb{R} \rightarrow & \mathbb{R}\\
x&\mapsto & x^2 & x\mapsto & x+2
\end{eqnarray*}[/tex]
É possível definir [tex]f\circ g~[/tex] e [tex]~g\circ f[/tex]?
► Observe inicialmente que [tex]x^2 \geqslant 0[/tex] para todo [tex]x \in \mathbb{R}[/tex]; portanto, [tex]Im(f)=\{y \in \mathbb{R}~|~y \geqslant 0\}. [/tex]
Com isso, [tex]Im(f)\subset D(g)=\mathbb{R}[/tex] e a função [tex]~g\circ f[/tex] está definida.
Agora, note que:
[tex]\qquad \left(g\circ f\right)(x)=g\left(f(x)\right)=g\left(x^2\right)=x^2+2.[/tex]
Logo, temos:
[tex]\qquad g\circ f:\mathbb{R}\rightarrow \mathbb{R}\\
\qquad \left(g\circ f\right)(x)=x^2+2.
[/tex]
► Observe, agora, que [tex]x+2 \in \mathbb{R}[/tex] para todo [tex]x \in \mathbb{R}[/tex]; portanto, [tex]Im(g)\subset\mathbb{R}. [/tex]
Com isso, [tex]Im(g)\subset D(f)=\mathbb{R}[/tex] e a função [tex]~f\circ g[/tex] também está definida:
[tex]\qquad \left(f\circ g\right)(x)=f\left(g(x)\right)=f\left(x+2\right)=\left(x+2\right)^2.[/tex]
Logo, temos:
[tex]\qquad f\circ g:\mathbb{R}\rightarrow \mathbb{R}\\
\qquad \left(f\circ g\right)=x^2+2x+4.
[/tex]
Observe que, embora as duas compostas estejam definidas, elas são distintas!
[tex]\qquad f(x)=2x-5\quad[/tex] e [tex]\quad g(x)=x+20[/tex], determine o valor de:
a) [tex]\textcolor{#BF7B3B}{ \left(f\circ g\right)(2)}=f(g(2))=f(22)=2\times 22-5=44-5=39.[/tex]
b) [tex]\textcolor{#BF7B3B}{ \left(g\circ f\right)(0)}=g(f(0))=g(0-5)=g(-5)=-5+20=15.[/tex]
c) [tex]\textcolor{#BF7B3B}{ \left(f\circ f\right)(1)}=f(f(1))=f(-3)=-11.[/tex]
d) [tex]\textcolor{#BF7B3B}{ \left(g\circ g\right)(5)}=g(g(5))=g(25)=45.[/tex]
e) [tex]\textcolor{#BF7B3B}{\left(g\circ g\circ g\right)(3)}=g(g(g(3)))=g(g(23))=g(43)=63.[/tex]
Desprezando-se a resistência do ar e considerando-se que a aceleração da gravidade é de [tex]g=10 \text{ m/s}^2[/tex], então, a cada instante [tex]t[/tex] dado em segundos, sua altura em relação à superfície da terra é dada em metros pela função [tex]h[/tex] definida por
[tex]\qquad h(t)=-\dfrac{g}{2}\,t^2+v_0t\\
\qquad \boxed{h(t)=-5t^2+30t}.[/tex]
E se fosse necessário determinarmos a altura do corpo a partir do tempo dado em minutos?
► Para converter minutos em segundos, podemos utilizar a função [tex]c[/tex] definida por
[tex] \qquad c(t)=60t[/tex]
com [tex]t[/tex] dado em minutos.
Dessa forma, a função composta [tex]h\circ c[/tex] nos dá a altura do corpo a partir do tempo [tex]t[/tex] dado em minutos. Se denotarmos essa composta por [tex]k[/tex], segue que:
[tex]\quad k(t)=\left(h\circ c\right)(t)=h(c(t))\\
\quad k(t)=h(60t)=-5\left(60t\right)^2+30(60t)\\
\quad k(t)=18000t^2+1800t.[/tex]
Assim, a altura em metros do corpo em relação à superfície da terra a cada instante [tex]t[/tex] dado em minutos é dada pela função [tex]k[/tex] definida por [tex]\boxed{k(t)=18000t^2+1800t}.[/tex]
[tex]~~ f(x)=\dfrac{2-x}{x}[/tex] ; [tex]g(x)=\sqrt[3]{x+1}-2[/tex] ; [tex]h(x)=(x+2)^3-1[/tex] ; [tex]t(x)=\dfrac{2}{x+1}.[/tex]
Qual a lei de formação da composta [tex] f \circ g \circ h \circ t[/tex]?
► Observe o desenvolvimento a seguir:
[tex]\qquad \begin{align*} \left(f \circ g \circ h \circ t\right)(x)&=f(g(h(t(x))))\\
&=f\left(g\left(h\left(\dfrac{2}{x+1}\right)\right)\right)\\
&=f\left(g\left(\left(\dfrac{2}{x+1}+2\right)^3-1\right)\right)\\
&=f\left(\sqrt[3]{\left(\left(\dfrac{2}{x+1}+2\right)^3-1\right)+1~}-2\right)\\
&=f\left(\sqrt[3]{\left(\dfrac{2}{x+1}+2\right)^3}-2\right)\\
&=f\left(\left(\dfrac{2}{x+1}+2\right)-2\right)\\
&=f\left(\dfrac{2}{x+1}\right)\\
&=\dfrac{2-\dfrac{2}{x+1}}{\dfrac{2}{x+1}}=\dfrac{\dfrac{2x+2-2}{x+1}}{\dfrac{2}{x+1}}=\dfrac{\dfrac{2x}{\cancel{x+1}}}{\dfrac{2}{\cancel{x+1}}}\\
&=\dfrac{2x}{2}=x
\end{align*} [/tex]
Portanto, [tex]\left(f \circ g \circ h \circ t\right)(x)=x.[/tex]
Suponhamos que [tex]f[/tex] seja a função que nos dá o tamanho da população desses peixes grandes, a partir do número [tex]n[/tex] de peixes pequenos presentes no rio, e [tex]g[/tex] seja a função que expressa o número desses peixes pequenos, a partir da quantidade [tex]x[/tex] de plânctons do rio.
Expresse o tamanho da população de peixes grandes em função da quantidade de plâncton, sabendo que:
[tex]\qquad \qquad f(n)=40+\sqrt{\dfrac{n+1}{120}}\quad [/tex] e [tex]\quad g(x)=4x+5.[/tex]
► Observe que, pelos dados do problema, [tex]n=g(x)[/tex]; assim, basta substituir [tex]n[/tex] por [tex]g(x)[/tex] na expressão [tex]f(n)[/tex], ou seja, a partir da composta [tex]f\circ g[/tex] teremos o tamanho da população da espécie de peixes grandes do rio em função da quantidade de plânctons. Vamos aos cálculos:
[tex]\qquad f(n)=40+\sqrt{\dfrac{n+1}{120}}\\
\qquad f(g(x))=40+\sqrt{\dfrac{4x+5+1}{120}}\\
\qquad f(g(x))=40+\sqrt{\dfrac{4x+6}{120}}\\
\qquad \boxed{f(g(x))=40+\sqrt{\dfrac{2x+3}{60}}}.[/tex]
Deste modo, determinar o valor de [tex]f(f(2))[/tex].
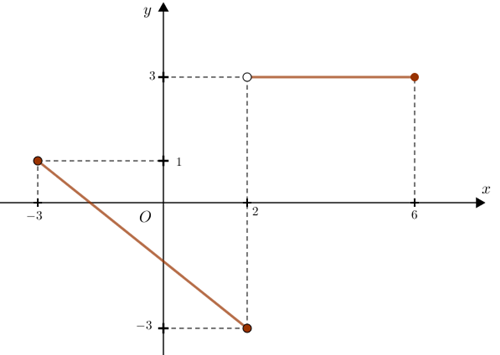
► Observando o gráfico, temos que:
[tex]\quad \textcolor{#98622F}{(i)~}f(2)=-3[/tex]
[tex]\quad \textcolor{#98622F}{(ii)~}f(-3)=1.[/tex]
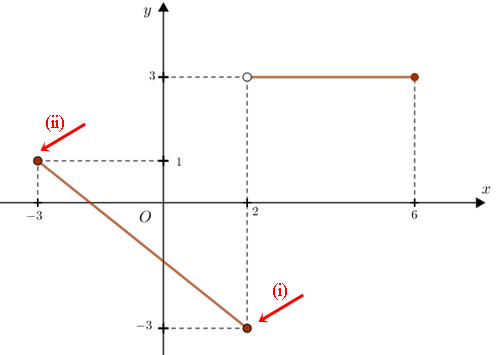
Portanto,
[tex]\quad \boxed{f(f(2))=f(-3)=1}.[/tex]
– [tex]C[/tex], a taxa média diária de monóxido de carbono no ar, em partes por milhão, corresponde a [tex]C(p)=0,5p+1[/tex];
– em um determinado tempo [tex]t[/tex], em anos, [tex]p[/tex] será igual a [tex]p(t)=10+0,1t^2.[/tex]
Em relação à taxa [tex]C:[/tex]
a) expresse-a como uma função de tempo;
b) calcule em quantos anos essa taxa será de [tex]13,2 [/tex] partes por milhão.
a) A taxa média diária de monóxido de carbono no ar em função da população [tex]p[/tex] é dada por [tex]C(p)=0,5p+1.[/tex]
Por outro lado, a população [tex]p[/tex] em um determinado tempo [tex]t[/tex] é dada por [tex]p(t)=10+0,1t^2.[/tex]
Assim, fazendo a composição das funções [tex]C[/tex] e [tex]p[/tex], teremos a taxa [tex]C[/tex] expressa como função do tempo [tex]t.[/tex]
Vamos aos cálculos:
[tex]\qquad C(t)=C(p(t))\\
\qquad C(t)= 0,5p(t)+1\\
\qquad C(t)= 0,5\left(10+0,1t^2\right)+1\\
\qquad C(t)= \left(5+0,05t^2\right)+1\\
\qquad \boxed{C(t)= 6+0,05t^2}.[/tex]
b) Fazendo [tex]C(t)=13,2 [/tex] na expressão resultante do item anterior, segue que:
[tex]\qquad C(t)=6+0,05t^2\\
\qquad 13,2=6+0,05t^2\\
\qquad 7,2=0,05t^2\\
\qquad t^2=\dfrac{7,2}{0,05}\\
\qquad t^2=144.[/tex]
Como [tex]t\gt 0[/tex], concluímos que [tex]t=12[/tex] anos.
Determine o valor da soma [tex]f(g(1))+g(f(–2)).[/tex]
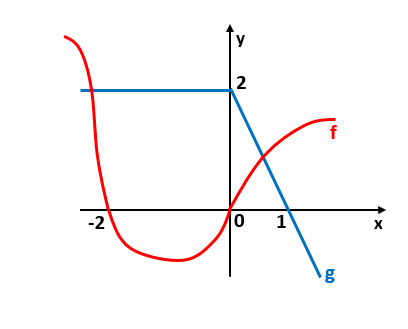
► Observando o gráfico das funções [tex]f[/tex] e [tex]g[/tex], segue que:
[tex]\quad \textcolor{#98622F}{(i)~}g(1)=0[/tex]
[tex]\quad \textcolor{#98622F}{(ii)~}f(-2)=0[/tex]
[tex]\quad \textcolor{#98622F}{(iii)~}f(g(1))+g(f(–2))=f(0)+g(0)[/tex]
[tex]\quad \textcolor{#98622F}{(iv)~}f(0)=0[/tex]
[tex]\quad \textcolor{#98622F}{(v)~}g(0)=2.[/tex]
Assim:
[tex]\qquad f(g(1))+g(f(–2))=f(0)+g(0)=0+2=2.[/tex]
a) [tex]2x^2+1\qquad [/tex] b) [tex](x/2)-1\qquad [/tex] c) [tex]x^2/2\qquad [/tex] d) [tex]x+1\qquad [/tex] e) [tex]x+(1/2)[/tex]
► Por definição de função composta,
[tex]\qquad f(g(x))=2g(x)-1[/tex]
e pelos dados do problema,
[tex]\qquad f(g(x))=x^2-1.[/tex]
Logo, segue que:
[tex]\qquad 2g(x)-1=x^2-1\\
\qquad 2g(x)=x^2\\
\qquad g(x)=\dfrac{x^2}{2}.\\
[/tex]
Portanto o item correto é o item c.
Se [tex]f(g(x))=g(f(x))[/tex], determine [tex]f(m).[/tex]
► Por definição de função composta, temos que:
[tex]\qquad f\left(g(x)\right)=2g(x)+3=2\cdot(3x+ m)+3\\
\qquad f\left(g(x)\right)=6x+2m+3[/tex]
e
[tex]\qquad g\left(f(x)\right)=3f(x)+ m=3\cdot (2x+3)+ m\\
\qquad g\left(f(x)\right)=6x+9+m.\\
[/tex]
Como [tex]f(g(x))=g(f(x))[/tex], segue que:
[tex] \qquad 6x+2m+3=6x+9+m\\
\qquad 2m+3=9+m \\
\qquad m=6.[/tex]
Com isso:
[tex]\qquad \boxed{f(6)=12+3=15}.[/tex]
