✏ Link da Sala para dispositivos da Apple.
Matematicamente, entendemos por grandeza tudo que pode ser medido ou contado; assim, são exemplos de grandezas o comprimento, a superfície, o volume, a massa, a capacidade, a velocidade, a temperatura, o tempo, entre outras.
É bastante comum no nosso dia a dia nos depararmos com situações que envolvam duas ou mais grandezas. Em algumas situações essas grandezas não se relacionam entre si; mas, em outras, as grandezas se relacionam. Observe os próximos exemplos.
 Imagem extraída de Pixabay.
Imagem extraída de Pixabay.
Não é possível relacionar a grandeza quantidade de casas da rua à grandeza quantidade de moradores.
Exemplo 2: Uma partida de futebol dura 90 minutos. Com 30 minutos de jogo, o placar é 1×0. Será que com 60 minutos o placar vai duplicar? Com 90 minutos o placar vai triplicar?
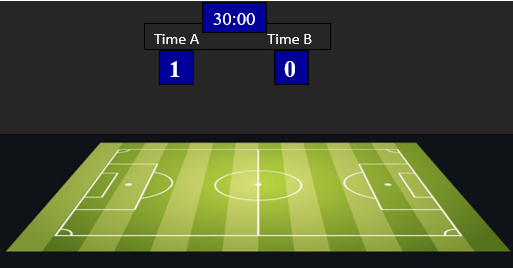 Imagem adaptada de Freepik.
Imagem adaptada de Freepik.
Provavelmente, não! Não há relação alguma entre as grandezas tempo de jogo e placar. Observe que o time que está perdendo pode, inclusive, “virar” o jogo e ganhar!
Exemplo 3: Se um bebê com um mês mede 53,5 cm, não podemos prever com exatidão qual será a sua altura com dois meses, ou aos cinco meses…
Portanto, também não há relação, de fato, entre as grandezas idade e altura.
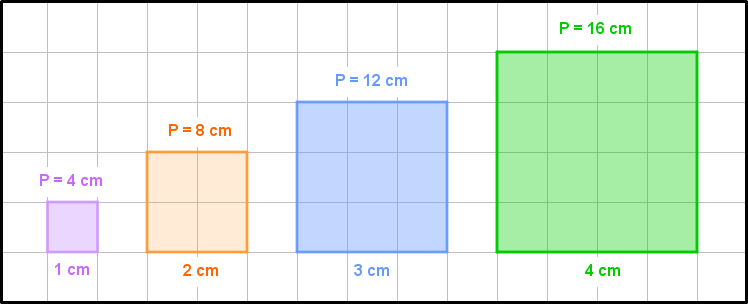
Aqui, existe uma relação entre a medida dos lados de um quadrado e a medida de seu perímetro, pois:
● se dobramos a medida dos lados de um quadrado, seu perímetro também dobra;
● se triplicamos a medida dos lados de um quadrado, seu perímetro também triplica;
● se quadruplicamos a medida dos lados de um quadrado, seu perímetro também quadruplica;
… e assim por diante.
Assim, as grandezas comprimento do lado do quadrado e perímetro do quadrado estão relacionadas.
Exemplo 5: Na tabela baixo, vemos o volume de água despejada em um recipiente com a forma de um cilindro reto e a respectiva altura que a água atingiu.

Os dados da tabela mostram que, neste caso, as grandezas volume e altura estão relacionadas, já que:
● se dobrarmos o volume d’água, a altura que ela ocupa no recipiente dobra;
● se triplicarmos o volume d’água, a altura que ela ocupa no recipiente triplica;
● se quintuplicarmos o volume d’água, a altura que ela ocupa no recipiente quintuplica;
… e assim sucessivamente.
Exemplo 6: O valor do prêmio principal do próximo sorteio da Mega-Sena está acumulado!
Assim, se apenas um apostador acertar os números sorteados ele receberá R$ 33.000.000,00. Se dois apostadores acertarem os números, cada um receberá um prêmio de R$ 16.500.000,00. Se três apostadores dividirem o prêmio, cada um levará R$ 11.000.000,00. Para quatro acertadores, o prêmio de cada um será de R$ 8.250.000,00.

Neste exemplo, as grandezas quantidade de acertadores e valor do prêmio estão relacionadas, já que para dois acertadores o prêmio é a metade do valor acumulado. Para três acertadores, o prêmio é um terço do valor acumulado. Para quatro acertadores, um quarto do valor acumulado, e assim por diante!
Exemplo 7: A fábrica do seu João tem 10 máquinas do mesmo tipo e com igual produção. Quando 2 máquinas são ligadas, elas produzem juntas 15 732 parafusos por dia. Se 5 máquinas forem ligadas, elas produzirão juntas 39 330 parafusos por dia. Com 6 máquinas ligadas, a produção diária será de 47 196 parafusos. Com 9 máquinas ligadas, a produção diária será de 70 794 parafusos.
A quantidade de máquinas ligadas e o número de parafusos produzidos estão relacionados?

Se você está com dificuldade para perceber que, de fato, as duas grandezas quantidade de máquinas ligadas e quantidade diária de parafusos produzidos estão relacionadas, perceba que:
● se aumentar a quantidade de máquinas em 2,5 vezes (de 2 para 5) a quantidade de parafusos também aumenta 2,5 vezes (de 15 732 para 39 330);
● se aumentar a quantidade de máquinas em 3 vezes (de 2 para 6) a quantidade de parafusos também aumenta 3 vezes (de 15 732 para 47 196);
● se aumentar a quantidade de máquinas em 4,5 vezes (de 2 para 9) a quantidade de parafusos também aumenta 4,5 vezes (de 15 732 para 70 794).
Nesta Sala vamos trabalhar apenas com grandezas como as dos Exemplos 4, 5, 6 e 7, isto é, com grandezas cujas medidas estão relacionadas de uma forma especial. Vamos ver como!
Numericamente, duas dessas grandezas, dadas em uma certa ordem, são representadas por uma razão entre as suas medidas correspondentes. (Entenderemos como razão de [tex]a[/tex] para [tex]b[/tex] o quociente [tex]\dfrac{a}{b}[/tex], com [tex]a,b\in \mathbb{R}[/tex] e [tex]b\ne 0.[/tex])
► Se as grandezas que definem a razão são de uma mesma espécie, devemos apresentá-las em uma mesma unidade. Neste caso, a razão será um número sem unidade de medida, como no Exemplo 4: as razões entre o comprimento do lado do quadrado e o perímetro desse quadrado são representadas respectivamente por [tex]\dfrac{1}{4}[/tex]; [tex]\dfrac{2}{8}[/tex]; [tex]\dfrac{3}{12}[/tex]; [tex]\dfrac{4}{16}[/tex]; etc.
► Se as grandezas que definem a razão não são de uma mesma espécie, essa razão terá uma unidade que vai depender das unidades das grandezas do numerador (antecedente) e do denominador (consequente) da razão. No caso do Exemplo 5; as razões entre o volume de água despejada e a altura que a água atingiu são representadas respectivamente por: [tex]\dfrac{1}{2,5}\text{ litro/cm}[/tex]; [tex]\dfrac{2}{5}\text{ litro/cm}[/tex] e [tex]\dfrac{3}{7,5}\text{ litro/cm}.[/tex]
Observe, mais um exemplo.
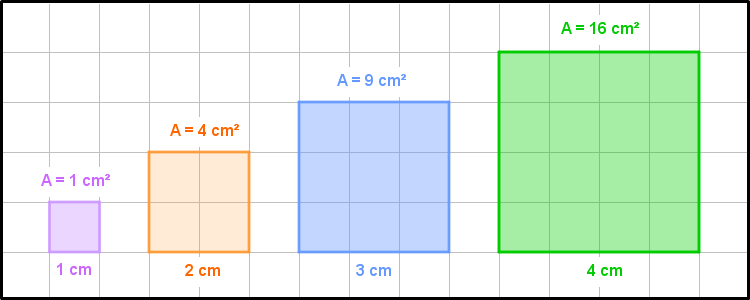
Aqui, existe uma relação entre a medida dos lados de um quadrado e a medida da sua área, já que
● se a medida dos lados de um quadrado for [tex]l[/tex], sua área será [tex]l^2.[/tex]
Assim, as grandezas comprimento e área estão relacionadas e podemos até definir uma razão entre essas medidas: [tex]\dfrac{l}{l^2}.[/tex]
Observe que a diferença entre o Exemplo 8 e, em particular, o Exemplo 4 está em três palavrinhas:
► quando o comprimento do lado do quadrado aumenta, a sua área aumenta;
► quando o comprimento do lado do quadrado aumenta, o seu perímetro aumenta “na mesma proporção“.
Numericamente:
● Exemplo 4: [tex]\dfrac{1}{4}=\dfrac{2}{8}=\dfrac{3}{12}=\dfrac{4}{16}.\\
[/tex]
● Exemplo 8: [tex]\dfrac{1}{1}\ne\dfrac{2}{4}\ne\dfrac{3}{9}\ne\dfrac{4}{16}.\\
[/tex]
Nos Exemplos 5 e 7 as variações aumentam também na mesma proporção:
● Exemplo 5: [tex]\dfrac{1}{2,5}=\dfrac{2}{5}=\dfrac{3}{7,5}.\\
[/tex]
● Exemplo 7: [tex]\dfrac{2}{15732}=\dfrac{5}{39330}=\dfrac{6}{47196}=\dfrac{9}{70794}.\\
[/tex]
No Exemplo 6 as variações também estão relacionadas e na mesma proporção. Isso mesmo, só que não de maneira direta como nos Exemplos 4, 5 e 7, mas sim de uma maneira inversa:
● se o número de ganhadores dobra, o valor do prêmio fica reduzido à metade;
● se o número de ganhadores triplica, o valor do prêmio fica reduzido à terça parte;
● se o número de ganhadores quadruplica, o valor do prêmio fica reduzido à quarta parte; etc.
Observe como indicamos a proporção:
● Exemplo 6: [tex]\dfrac{1}{\frac{1}{33000000}}=\dfrac{2}{\frac{1}{16500000}}=\dfrac{3}{\frac{1}{11000000}}=\dfrac{4}{\frac{1}{8250000}}.\\
[/tex]
As grandezas envolvidas nos Exemplos 4, 5, 6 e 7 são chamadas de grandezas proporcionais e podem ser de dois tipos, conforme veremos nas duas situações a seguir.
Neste caso, as grandezas envolvidas são tempo e produção.
 Imagem extraída de Freepik.
Imagem extraída de Freepik.
Na situação acima, suponha que a produção do operário seja constante ao longo do dia, produzindo [tex]n[/tex] peças a cada hora. Então, trabalhando [tex]6[/tex] horas, no final do dia terá produzido [tex]6n[/tex] peças. Trabalhando uma hora a mais, ou seja, [tex]7[/tex] horas durante o dia, ao final ele terá produzido [tex]7n[/tex] peças; trabalhando [tex]8[/tex] horas, ele produzirá [tex]8n[/tex] peças; e assim por diante.
Como se pode perceber, à medida que aumenta a quantidade de horas trabalhadas, o número de peças produzidas também aumenta, e na mesma proporção, ou seja, se forem trabalhadas [tex]h[/tex] horas, podemos concluir que serão produzidas [tex]h\cdot n[/tex] peças. Dizemos, neste caso, que as duas grandezas envolvidas são diretamente proporcionais.
 Imagem extraída de LANCE!.
Imagem extraída de LANCE!.
Nesta segunda situação, vemos que quanto maior a velocidade, menor será o tempo gasto.
Suponha que um atleta complete todo o percurso em [tex]h[/tex] horas, com uma velocidade [tex]v[/tex] km/h. Então o comprimento do trajeto é de [tex]h\cdot v[/tex] km. Se um segundo atleta corre a uma velocidade [tex]2v[/tex] km/h, ele completará o percurso em [tex]\dfrac{h\cdot v}{2v} = \dfrac{h}{2}[/tex] horas. Se um terceiro atleta corre a uma velocidade [tex]3v[/tex] km/h, ele completará o percurso em [tex]\dfrac{h\cdot v}{3v} = \dfrac{h}{3}[/tex] horas. Como se pode observar, à medida que a velocidade aumenta, o tempo diminui (na mesma proporção). Por isso, dizemos que, nesta situação, as duas grandezas envolvidas são inversamente proporcionais.
Assim, as duas grandezas dos Exemplos 4, 5 e 7 são diretamente proporcionais e as do Exemplo 6 são inversamente proporcionais. São esses os dois tipos de grandezas que discutiremos daqui para frente.
Uma observação importante: nesta Sala estudaremos grandezas associadas apenas a medidas positivas, embora existam grandezas que possam ser associadas a medidas negativas como, por exemplo, a temperatura.
Grandezas Diretamente Proporcionais
Ainda sobre a primeira situação da seção anterior, se o operário produz 30 unidades de determinada peça em um período de 6 horas, então ele produz 5 peças a cada hora. Assim, em 7 horas, por exemplo, ele produziria [tex]7\times 5 = 35[/tex] peças, e em 8 horas produziria [tex]8\times 5 = 40[/tex] peças, conforme ilustrado na tabela abaixo.
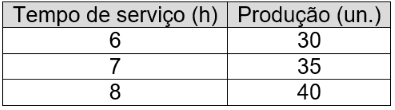
A razão entre dois valores da grandeza Tempo é igual à razão entre os dois valores correspondentes da grandeza Produção. É isso que determina, matematicamente, que essas grandezas são diretamente proporcionais.
Definição: Duas grandezas são ditas diretamente proporcionais quando a razão entre dois valores quaisquer da primeira é igual à razão entre os dois valores correspondentes da segunda.
Vamos tentar olhar de outra forma essa definição.
Considere duas grandezas [tex]X[/tex] e [tex]Y[/tex] diretamente proporcionais.
Sejam [tex]x_1,\;x_2,\, x_3, \text{ etc.}[/tex] valores quaisquer assumidos por [tex]X[/tex] e [tex]y_1,\;y_2,\,y_3, \text{ etc.}[/tex] os valores correspondentes assumidos por [tex]Y[/tex]; como [tex]X[/tex] e [tex]Y[/tex] são diretamente proporcionais, então, particularmente:
[tex]\qquad \dfrac{x_1}{x_2}=\dfrac{y_1}{y_2}[/tex], [tex]\quad \dfrac{x_1}{x_3}=\dfrac{y_1}{y_3}[/tex], [tex]\quad \dfrac{x_1}{x_4}=\dfrac{y_1}{y_4}[/tex], etc.
Com isso,
[tex]\qquad \dfrac{y_1}{x_1}=\dfrac{y_2}{x_2}[/tex], [tex]\quad \dfrac{y_1}{x_1}=\dfrac{y_3}{x_3}[/tex], [tex]\quad \dfrac{y_1}{x_1}=\dfrac{y_4}{x_4}[/tex], etc.
e, dessa forma, segue que
[tex]\qquad \dfrac{y_1}{x_1}=\dfrac{y_2}{x_2}=\dfrac{y_3}{x_3}=\dfrac{y_4}{x_4}=\cdots [/tex]
Se o valor comum desses quocientes for igual à constante (positiva) [tex]k[/tex], então, para qualquer valor [tex]x[/tex] da grandeza [tex]X[/tex] e o seu valor correspondente [tex]y[/tex] da grandeza [tex]Y[/tex], teremos [tex]\dfrac{y}{x}=k[/tex], ou ainda, [tex]y=kx.[/tex]
Assim,
Duas grandezas [tex]X[/tex] e [tex]Y[/tex] são ditas diretamente proporcionais quando existir uma constante [tex]k[/tex] positiva, denominada constante de proporcionalidade, tal que [tex]\,\dfrac{y}{x} = k\,[/tex] (ou [tex]y=kx[/tex]), para qualquer valor [tex]x[/tex] da grandeza [tex]X[/tex] e o seu valor correspondente [tex]y[/tex] da grandeza [tex]Y.[/tex]
Observe que a existência de uma constante positiva [tex]k[/tex] tal que [tex]\boxed{y=kx}[/tex] para qualquer valor [tex]x[/tex] da grandeza [tex]X[/tex] e o valor correspondente [tex]y[/tex] da grandeza [tex]Y[/tex] nos garante, à primeira vista, que os valores de duas grandezas diretamente proporcionais aumentam ou diminuem simultaneamente. No entanto, o Exemplo 8 nos mostra que os valores de duas grandezas podem aumentar ou diminuir simultaneamente sem que sejam diretamente proporcionais ou mesmo proporcionais!
Mas não se preocupe; o que a igualdade [tex]y=kx[/tex] garante, de fato, é que duas grandezas são diretamente proporcionais quando, aumentando os valores de uma delas, os valores correspondentes da outra também aumentam na mesma proporção, ou diminuindo os valores de uma delas, os valores correspondentes da outra também diminuem na mesma proporção. E isso confirma as observações feitas quando discutimos os exemplos iniciais. Se você não conseguiu ver o aumento ou a diminuição na mesma proporcionalidade, clique no botão abaixo.
Como sabemos que os valores de duas grandezas [tex]X[/tex] e [tex]Y[/tex] diretamente proporcionais estão relacionados por meio da expressão algébrica [tex]y=kx[/tex], na qual [tex]k[/tex] é uma constante positiva e tanto [tex]x[/tex] quanto [tex]y[/tex] podem assumir valores reais positivos, podemos representar graficamente a relação entre duas grandezas diretamente proporcionais [tex]X[/tex] e [tex]Y[/tex] em um plano cartesiano [tex]xOy[/tex] e obteremos pontos cujas coordenadas são [tex]\left(x,kx \right)[/tex], para valores [tex]x[/tex] da grandeza [tex]X[/tex], e que estarão alinhados. Particularmente, quando [tex]x,y \in \mathbb{R}^*_+[/tex], o gráfico será uma semirreta que parte da origem do sistema cartesiano (mas o ponto [tex]\left(0,0\right)[/tex] não faz parte dela).
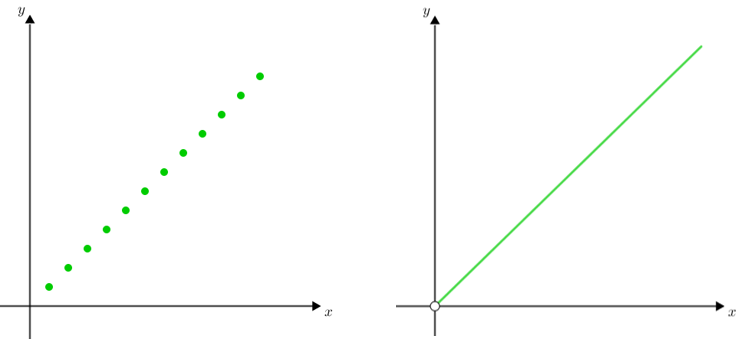
Grandezas Inversamente Proporcionais
Agora, vamos analisar melhor a segunda situação da Introdução.
Considere que um atleta leve 1 hora para percorrer um determinado trecho a uma velocidade constante de 5 km/h. Se outro atleta correr esse mesmo trecho duas vezes mais rápido, certamente ele levará metade do tempo do primeiro atleta, ou seja, levará 1/2 hora percorrendo a uma velocidade de 10 km/h. E, da mesma forma, se um terceiro atleta percorresse o mesmo trecho três vezes mais rápido que o primeiro, ele levaria 1/3 do tempo deste, ou seja, ele faria o mesmo percurso em 1/3 hora, percorrendo a uma velocidade de 15 km/h. Observe a tabela abaixo.
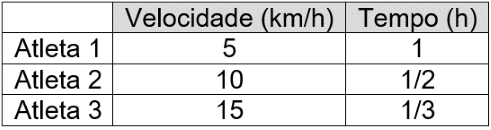
Perceba que a razão entre dois valores da grandeza Velocidade é igual ao inverso da razão entre os dois valores correspondentes da grandeza Tempo; e é isso que determina, matematicamente, que essas grandezas são inversamente proporcionais.
Definição: Duas grandezas são ditas inversamente proporcionais quando a razão entre dois valores quaisquer da primeira é igual ao inverso da razão entre os valores correspondentes da segunda.
Podemos também olhar de outra forma essa definição.
Considere duas grandezas [tex]X[/tex] e [tex]Y[/tex] inversamente proporcionais.
Se [tex]x_1,\;x_2,\, x_3, \text{ etc.}[/tex] forem valores quaisquer assumidos pela grandeza [tex]X[/tex] e [tex]y_1,\;y_2,\,y_3, \text{ etc.}[/tex] forem os valores correspondentes assumidos por [tex]Y[/tex]; como [tex]X[/tex] e [tex]Y[/tex] são inversamente proporcionais, então, particularmente, teremos:
[tex]\qquad \dfrac{x_1}{x_2}= \left(\dfrac{y_1}{y_2}\right)^{-1}[/tex], [tex]\quad \dfrac{x_1}{x_3}= \left(\dfrac{y_1}{y_3}\right)^{-1}[/tex], [tex]\quad \dfrac{x_1}{x_4}= \left(\dfrac{y_1}{y_4}\right)^{-1}[/tex], etc.
ou seja,
[tex]\qquad \dfrac{x_1}{x_2}=\dfrac{y_2}{y_1}[/tex], [tex]\quad \dfrac{x_1}{x_3}=\dfrac{y_3}{y_1}[/tex], [tex]\quad \dfrac{x_1}{x_4}=\dfrac{y_4}{y_1}[/tex], etc.
Com isso,
[tex]\qquad x_1\cdot y_1=x_2 \cdot y_2[/tex], [tex]\quad x_1\cdot y_1=x_3 \cdot y_3[/tex], [tex]\quad x_1\cdot y_1=x_4 \cdot y_4[/tex], etc.
e, dessa forma, segue que
[tex]\qquad x_1\cdot y_1=x_2 \cdot y_2=x_3 \cdot y_3=x_4 \cdot y_4=\cdots\,[/tex] .
Se o valor comum desses produtos for a constante (positiva) [tex]k[/tex], então, para qualquer valor [tex]x[/tex] da grandeza [tex]X[/tex] e o seu valor correspondente [tex]y[/tex] da grandeza [tex]Y[/tex], teremos [tex]x\cdot y=k.[/tex]
Dessa forma,
Duas grandezas [tex]X[/tex] e [tex]Y[/tex] são ditas inversamente proporcionais quando existir uma constante [tex]k[/tex] positiva, denominada constante de proporcionalidade, tal que [tex]x\cdot y=k[/tex] (ou [tex]y=\dfrac{k}{x}[/tex]), para qualquer valor [tex]x[/tex] da grandeza [tex]X[/tex] e o seu valor correspondente [tex]y[/tex] da grandeza [tex]Y.[/tex]
Observe que a existência de uma constante positiva [tex]k[/tex] tal que [tex]\boxed{y=k\,\dfrac{1}{x}}[/tex] para qualquer valor [tex]x[/tex] da grandeza [tex]X[/tex] e o valor correspondente [tex]y[/tex] da grandeza [tex]Y[/tex] nos garante que, para duas grandezas inversamente proporcionais, aumentando os valores de uma delas, os valores da outra diminuem na mesma proporção ou, diminuindo os valores de uma delas, os valores da outra aumentam na mesma proporção.
Assim como na grandezas diretamente proporcionais, é importante lembrar que para as grandezas inversamente proporcionais os aumentos e as respectivas diminuições de valores são proporcionais.
Também podemos representar graficamente a expressão algébrica [tex] y=k\, \dfrac{1}{x}[/tex] que caracteriza duas grandezas inversamente proporcionais [tex]X[/tex] e [tex]Y[/tex] em um plano cartesiano [tex]xOy[/tex]. Aqui, obteremos pontos cujas coordenadas são [tex]\left(x,\dfrac{k}{x} \right)[/tex], para valores [tex]x[/tex] da grandeza [tex]X[/tex], que definem parte de uma curva conhecida como hipérbole. Particularmente, quando [tex]x,y \in \mathbb{R}^*_+[/tex], o gráfico será um ramo de hipérbole.
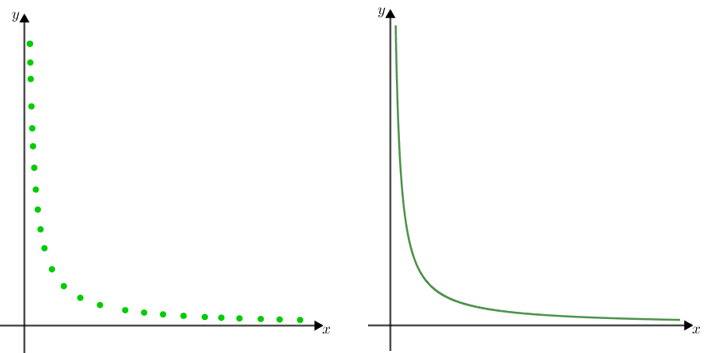
Se for o caso, acalme-se.
Muitos dos problemas de Matemática que envolvem proporcionalidade direta ou inversa entre duas grandezas podem ser resolvidos utilizando-se duas regras cujos nomes dão título à Sala 2: Regras de Três.
Para conhecê-las, é só clicar no botão Sala 2.
Bons estudos!!!
Equipe COM – OBMEP
Novembro de 2023.
[1] BIANCHINI, Edwaldo; MIANI, Marcos. Construindo conhecimentos em Matemática, 7ª série. São Paulo: Moderna, 2000.
[2] BIGODE, Antonio José Lopes; MIANI, Marcos. Matemática hoje é feita assim, 6ª série. 1ª Edição. São Paulo: FTD, 2000.
[3] BOYER, Carl Benjamin. História da Matemática, 3ª Edição. São Paulo: Edgard Blucher, 2010.
[4] EVES, Howard. Introdução à História da matemática. Campinas, SP: Editora da Unicamp, 2004.
[5] PAIVA, M. R. Moderna Plus. Matemática Paiva 1. 1a edição ed. [s.l.] Moderna, 2010.
[6] Portal da OBMEP. (Último acesso em 20/06/20).
