✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 2ª série do E. M.)
Um recipiente de vidro em formato cilíndrico tem 6 cm de altura e sua base é uma circunferência medindo 16 cm. Uma formiga está do lado de fora do copo, a 1 cm do topo, enquanto, do lado de dentro, a 5 cm do topo, está uma gota de mel.
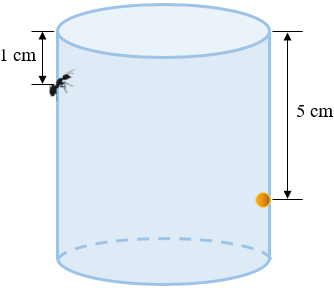
A gota e a formiga encontram-se em geratrizes do cilindro que são simétricas em relação ao eixo do cilindro. Qual a menor distância que a formiga deve andar para atingir a gota de mel?
Extraído de Escola Naval-Adaptado.
Solução
A imagem abaixo mostra a trajetória com menor distância que a formiga deve percorrer para alcançar o mel, sendo que o caminho tracejado é percorrido no interior do recipiente.
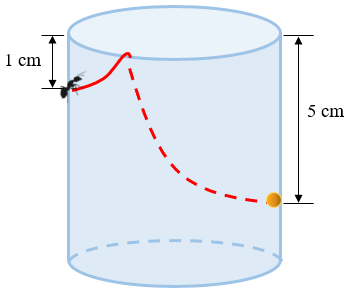
Como queremos a menor distância percorrida pela formiga, faremos uma planificação da lateral do cilindro (abrindo-o sem distorções), cortando-o pela geratriz que passa pela formiga; teremos, então, a seguinte situação:
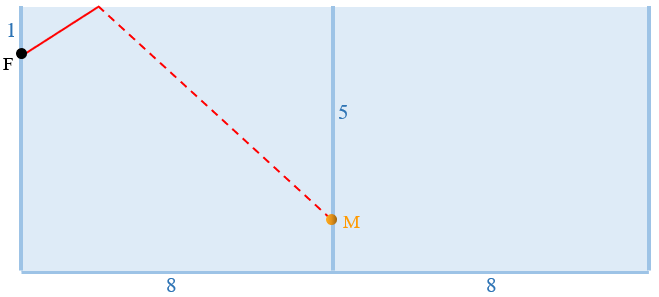
Agora que já conseguimos visualizar o menor caminho, vamos calcular a distância que a formiga vai percorrer. Para isso, vamos refletir o ponto F com relação ao segmento que corresponde à borda superior do recipiente de vidro: seja G o ponto refletido. Considere também o ponto B, interseção dessa “borda superior” com o segmento definido por G e M, conforme mostrado na próxima imagem.
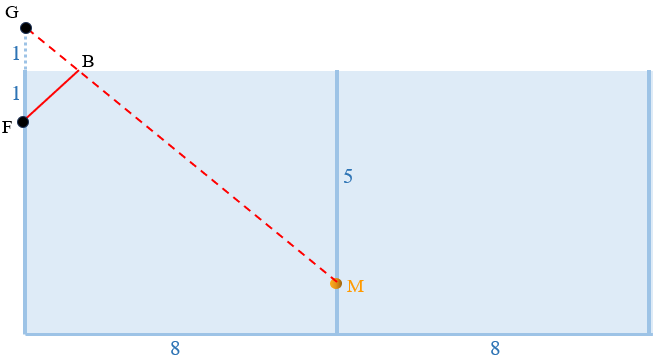
Perceba que os segmentos [tex]\overline{FB}[/tex] e [tex]\overline{GB}[/tex] têm o mesmo comprimento; logo, o comprimento do trajeto FBM é igual ao comprimento do segmento [tex]\overline{GM}[/tex], e este comprimento, que será denotado por [tex]GM[/tex], nós conseguimos calcular.
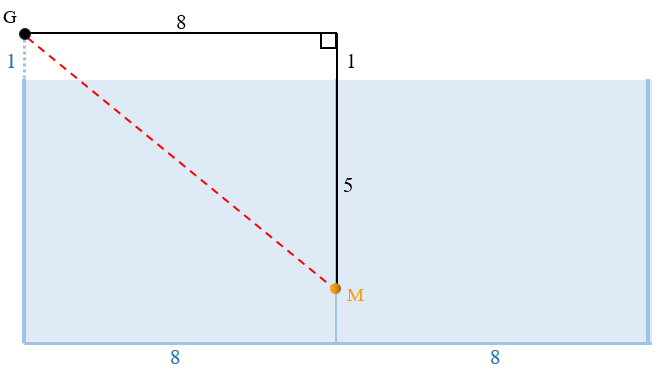
Note que o triângulo que aparece na modelagem do problema é um triângulo retângulo cujos catetos medem [tex]6\text{ cm }[/tex] e [tex]8\text{ cm}.[/tex] Aplicando-se o Teorema de Pitágoras, segue que:
[tex]\qquad GM^{2}=6^{2}+8^{2}\\
\qquad \boxed{GM=10\text{ cm}}\,.\\
~~[/tex]
Portanto, a menor distância que a formiga deve andar para atingir a gota de mel é de 10 centímetros.
Solução elaborada pelos Moderadores do Blog.
