Clique no botão abaixo para visualizar o problema.
Problema
Na figura abaixo vemos dois retângulos, o retângulo [tex]P[/tex] e o retângulo [tex]Q.[/tex]
Sabe-se que a região sombreada que aparece na figura corresponde a [tex]\dfrac{2}{5}[/tex] do retângulo [tex]P[/tex] e a [tex]\dfrac{1}{6}[/tex] do retângulo [tex]Q.[/tex]
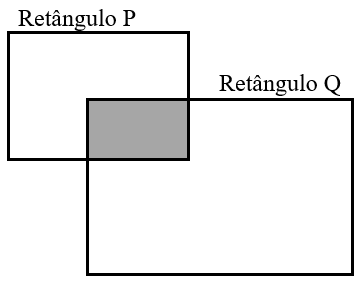
Se a área da parte sombreada é de [tex]182\text{ cm}^2[/tex], encontre a área de toda a figura, em [tex]\text{cm}^2.[/tex]
Solução
Vamos denotar por [tex]A_P~[/tex] e [tex]~A_Q[/tex] as áreas dos retângulos [tex]P[/tex] e [tex]Q[/tex], respectivamente.
Assim, pelos dados do problema, temos que:
[tex]\qquad \textcolor{#800000}{(i)}\, \dfrac{2}{5} A_P=182[/tex], donde [tex] \boxed{A_P=455\text{ cm}^2}.[/tex]
[tex]\qquad \textcolor{#800000}{(ii)}\, \dfrac{1}{6} Q_P=182[/tex], donde [tex] \boxed{A_Q=1092\text{ cm}^2}.[/tex]
Agora, perceba que, ao somarmos as áreas [tex]A_P~[/tex] e [tex]~A_Q[/tex], estaremos somando duas vezes a área sombreada. Portanto, a área de toda a figura é dada por:
[tex]\qquad A_{total}=A_P+A_Q-182=455+1092-182.[/tex]
Assim, a área de toda a figura é [tex] \fcolorbox{black}{#FFE3AA}{$1365\text{ cm}^2$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Primeira Gincana de 2023 – Clubes de Matemática da OBMEP
Nível A – Questão Difícil
Nível A – Questão Difícil
