Problema
(Indicado a partir do 2º ano do E. M.)
Seja [tex]ABC[/tex] um triângulo qualquer. Indicaremos por [tex]\hat{A}[/tex], [tex]\hat{B}[/tex] e [tex]\hat{C}[/tex] os seus ângulos internos e por [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] as medidas dos lados [tex]\overline{BC}[/tex], [tex]\overline{AC}[/tex] e [tex]\overline{AB}[/tex], respectivamente.
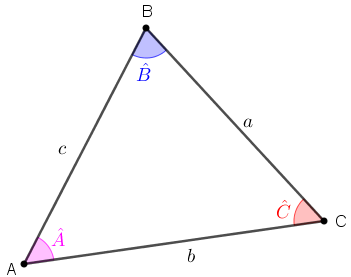
A lei dos cossenos nos diz que é válida a relação [tex]a^2 = b^2 + c^2-2bc \cdot cos \hat{A}[/tex]. Prove que também é válida a seguinte relação:
[tex]\qquad\qquad\boxed{sen^2 \hat{A} = sen^2 \hat{B} + sen^2 \hat{C}-2 \cdot sen\hat{B} \cdot sen\hat{C} \cdot cos\hat{A}}[/tex].
Solução
Da lei dos senos, temos [tex]\dfrac{a}{sen\hat{A}} = \dfrac{b}{sen\hat{B}} = \dfrac{c}{sen\hat{C}} = 2R[/tex], onde [tex]R[/tex] é o raio da circunferência circunscrita ao triângulo [tex]ABC[/tex].
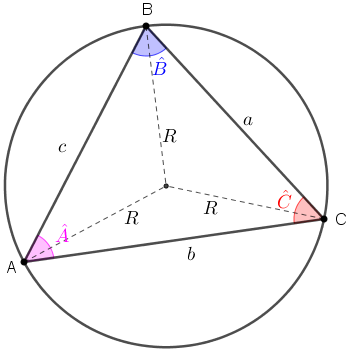
Assim, [tex]\boxed{a = 2R \cdot sen\hat{A}}[/tex], [tex]\boxed{b = 2R \cdot sen\hat{B}}[/tex] e [tex]\boxed{c = 2R \cdot sen\hat{C}}\,.[/tex]
Substituindo esses resultados em [tex]a^2 = b^2 + c^2-2bc \cdot cos \hat{A}[/tex], segue que:
[tex]~~ (2R \cdot sen\hat{A})^2 = (2R \cdot sen\hat{B})^2 + (2R \cdot sen\hat{C})^2-2 \cdot 2R \cdot sen\hat{B} \cdot 2R \cdot sen\hat{C} \cdot cos \hat{A}\\
~~ 4R^2 \cdot sen^2\hat{A} = 4R^2 \cdot sen^2\hat{B} + 4R^2 \cdot sen^2\hat{C}-2 \cdot 4R^2 \cdot sen\hat{B} \cdot sen\hat{C} \cdot cos \hat{A}\\
~~4R^2\cdot sen^2\hat{A} = 4R^2 \cdot (sen^2\hat{B} + sen^2\hat{C}-2 \cdot sen\hat{B} \cdot sen\hat{C} \cdot cos \hat{A}).[/tex]
Observe que [tex]R[/tex] é o raio de uma circunferência e, portanto, [tex]R\ne 0[/tex]. Então, segue da última igualdade que:
[tex] ~~\cancel{4R^2} \cdot sen^2\hat{A} = \cancel{4R^2} \cdot (sen^2\hat{B} + sen^2\hat{C}-2 \cdot sen\hat{B} \cdot sen\hat{C} \cdot cos \hat{A})\\
\qquad\fcolorbox{black}{#eee0e5}{$sen^2\hat{A} = sen^2\hat{B} + sen^2\hat{C}-2 \cdot sen\hat{B} \cdot sen\hat{C} \cdot cos \hat{A}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog .
