Problema
(Indicado a partir do 3º ano do E. M.)
Um professor deseja comprar uma geladeira cujo preço à vista é R$ 2 000,00.
O vendedor da loja explica que a compra pode ser feita a prazo em dez vezes mensais de igual valor, sendo o primeiro pagamento para um mês após a compra.
Sabendo que a loja cobra uma taxa de juros de 0,2% ao mês, qual é o valor da prestação?
Solução
Um princípio básico de Matemática Financeira é que quantias iguais em épocas diferentes tem valores diferentes. Assim, não faz sentido comparar quantias em épocas diferentes sem movimentá-las ao longo do tempo. Ao movimentar uma quantia no tempo, utilizamos dois fatores conhecidos como fator de capitalização, [tex]\boxed{FC=(1 + i)^n}[/tex], e fator de atualização, [tex]\boxed{FA=\dfrac{1}{(1 + i)^n}}.[/tex]
- Multiplicando uma quantia pelo fator de capitalização, obtemos o valor equivalente numa data futura (futuro valor FV), n períodos de tempo depois.
- Multiplicando uma quantia pelo fator de atualização, obtemos o valor equivalente numa data passada (presente valor PV), n períodos de tempo antes.
No nosso problema, devemos movimentar os dez pagamentos para a data zero, a fim de que possamos compará-los com o preço à vista da geladeira. Uma ideia seria aplicar o fator de atualização a cada um deles; entretanto, essa série uniforme de pagamentos pode ser movimentada de uma única vez para a data zero, obtendo o que chamamos de presente valor (PV) da série. Para isso, utiliza-se a fórmula [tex]\boxed{PV=PMT\;\dfrac{1-(1 + i)^{-n}}{i}}[/tex], sendo PMT o valor de cada prestação.
(Tente provar essa fórmula, usando soma de termos de uma progressão geométrica!)
Deste modo,
[tex]\quad \quad 2000 = PMT\cdot \dfrac{1-(1,002)^{-10}}{0,002} \\
\quad \quad PMT=\dfrac{2000\times 0,002}{1-(1,002)^{-10}} \\
\quad \quad PMT=\dfrac{4}{1-(1,002)^{-10}} \\
\quad \quad PMT\approx \dfrac{4}{1-0,9802183} \\
\quad \quad PMT\approx \dfrac{4}{0,0197817} \\
\quad \quad PMT\approx 202,21\,.\\[/tex]
Assim, o valor de cada prestação seria de, aproximadamente, [tex]\fcolorbox{black}{#eee0e5}{$ R\$\,202,21$}\,.[/tex]
O diagrama a seguir, conhecido como fluxo de caixa, ilustra o nosso problema.
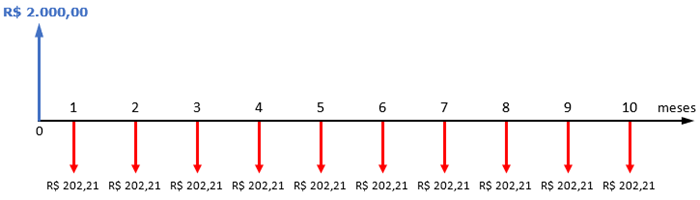
Solução elaborada pelos Moderadores do Blog.
