Problema
(Indicado a partir do 1º ano do E. M.)
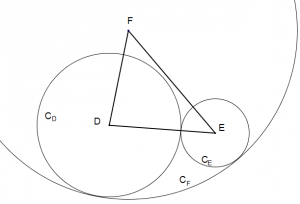
Considere três círculos [tex]C_D[/tex], [tex]C_E[/tex] e [tex]C_F[/tex] de centros [tex]D[/tex], [tex]E[/tex] e [tex]F[/tex], respectivamente.
Além disso, os círculos [tex]C_D[/tex] e [tex]C_E[/tex] são tangentes externos (entre si) e cada um deles é tangente interno a [tex]C_F[/tex].
Se o perímetro do triângulo de vértices [tex]D[/tex], [tex]E[/tex] e [tex]F[/tex] é [tex]30[/tex] centímetros, qual é a medida do raio do círculo [tex]C_F[/tex]?
Notação
✏ Denotaremos a distância entre dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]|XY|[/tex].
Solução
Vamos chamar de [tex]G[/tex] o ponto de tangência dos círculos [tex]C_D[/tex] e [tex]C_E[/tex]; [tex]G'[/tex] o ponto de tangência dos círculos [tex]C_D[/tex] e [tex]C_F[/tex] e [tex]G”[/tex] o ponto de tangência dos círculos [tex]C_E[/tex] e [tex]C_F[/tex].
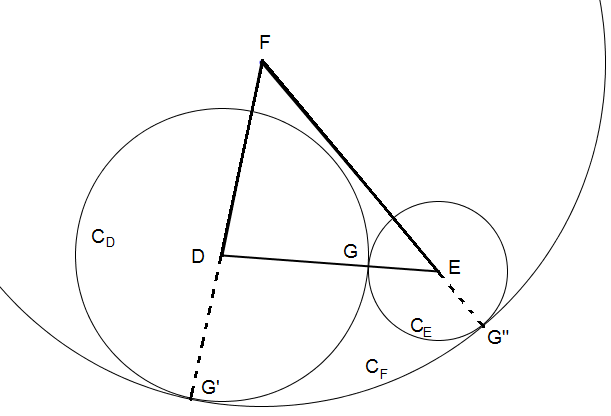
Observe que [tex]|DG’|=|DG|[/tex] e [tex]|EG”|=|EG|[/tex].
O raio [tex]R[/tex] do círculo [tex]C_F[/tex] pode ser obtido de duas maneiras:
[tex]\qquad\qquad R = |FD|+|DG’|= |FD|+|DG|[/tex]
[tex]\qquad\qquad R = |FE|+|EG”|= |FE|+|EG|.[/tex]
Portanto,
[tex]\qquad\qquad 2R = |FD|+|DG|+|FE|+|EG|\\
\qquad\qquad 2R = |FD|+(|DG|+|EG|)+|FE| \\
\qquad\qquad 2R=|FD|+|DE|+|FE|=30,[/tex]
ou seja,
[tex]\qquad\qquad R = 15[/tex].
Assim, o raio do círculo [tex]C_F[/tex] mede [tex]15[/tex] centímetros.
Solução elaborada pelos Moderadores do Blog .
Participaram da discussão os Clubes: Códigos infinitos; MIRIM APRENDIZ.