.Problema: Área total

Problema
(Indicado a partir do 2º ano do E. M.)

---

A coberta superior e as paredes retangulares laterais de um circo são revestidas com lona. Parte da estrutura do circo está mostrada na figura com suas medidas correspondentes. O piso não é revestido com lona.

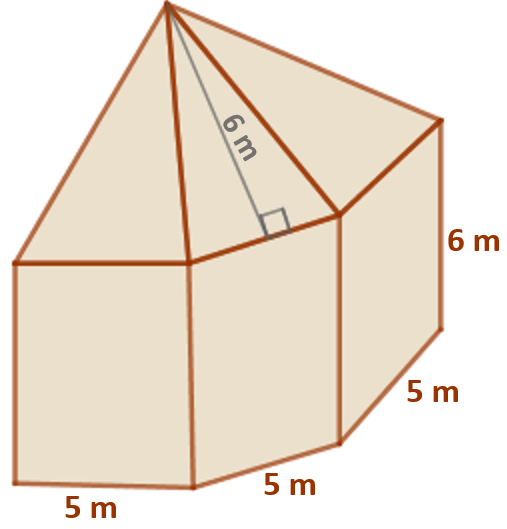
A pirâmide da parte superior dessa coberta é regular e possui [tex]21[/tex] vértices.
Calcular a área total da lona utilizada no revestimento da coberta e das paredes.

Solução

---

Inicialmente, observe que a pirâmide da coberta possui [tex]21[/tex] vértices, sendo um desses o vértice superior da pirâmide. Então, a pirâmide possui [tex]20[/tex] faces triangulares laterais e, consequentemente, o prisma que compõe as paredes possui [tex]20[/tex] faces retangulares laterais.
Dessa forma, a área total da lona, [tex]A_{T}[/tex], é dada pela soma das áreas dos vinte retângulos laterais com as áreas dos vinte triângulos que ficam na coberta.
Observe que:

► Para cada retângulo temos: [tex]~~\\ A_r=\text{base}\times\text{altura}=5 \times 6=30\text{ m}^2.\\ ~~[/tex]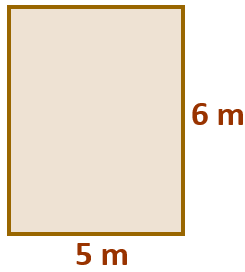

► Para cada triângulo temos: [tex]~~\\ A_t=\dfrac{\text{base}\times\text{altura}}{2}=\dfrac{5 \times 6}{2}=15\text{ m}^2.\\ ~~[/tex]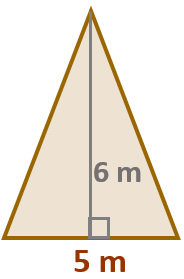

Assim, segue que:
[tex]\qquad \qquad A_T=20 \times A_r+20\times A_t \\
\qquad \qquad A_T=20 \times30+20\times 15 \\
\qquad \qquad A_T=600+300 \\
\qquad \qquad \boxed{A_T=900}\,. [/tex]
Portanto, foram utilizados [tex]\fcolorbox{black}{#EEE2D3}{$A_T=900\text{ m}^2$}[/tex] de lona no revestimento da coberta e das paredes do circo.

---

Solução elaborada pelos Moderadores do Blog.