(A) Problema de Gincana: Um ângulo da estrela

Problema

---

Cinco prédios de uma cidade estão posicionados de forma que cada um pode ser representado pelo vértice de um pentágono estrelado, conforme mostra a figura.

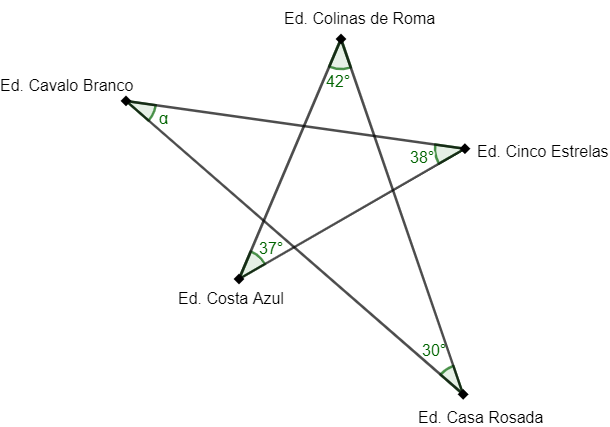
Qual a medida do ângulo [tex]\alpha[/tex], em graus?

Solução 1

---

Como ângulos opostos pelo vértice têm a mesma medida, podemos destacar as seguintes medidas de pares de ângulos na figura:

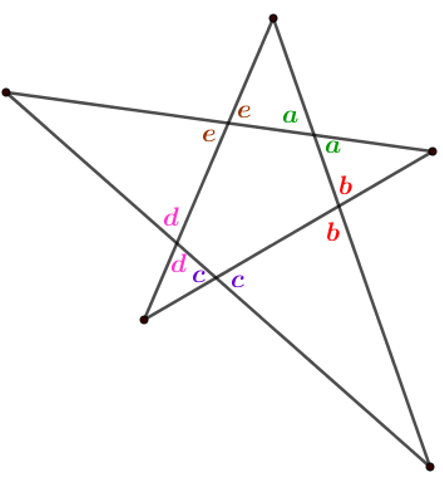
Observe que cada quíntupla [tex]a, b, c, d, e[/tex] corresponde a medidas de uma sequência de ângulos externos do pentágono que aparece no centro da figura. Como a soma das medidas dos ângulos externos de um polígono convexo é sempre [tex]360^\circ[/tex], concluímos que [tex]a+b+c+d+e=360^\circ[/tex].
Agora, note que em cada triângulo que forma uma ponta da estrela a soma das medidas dos ângulos internos é [tex]180^\circ[/tex].

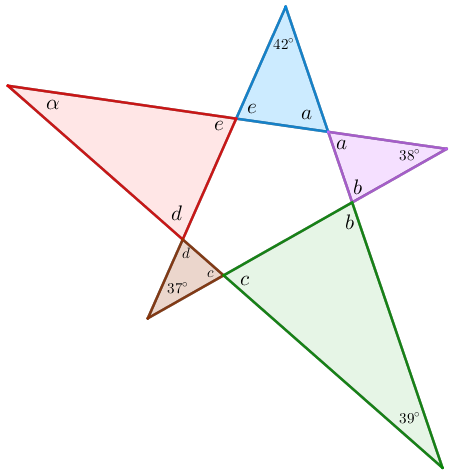
Logo, somando as medidas de todos os ângulos internos de todas as pontas, segue que:
[tex]\left(42^\circ+a+e\right)+\left(38^\circ+a+b\right)+\left(39^\circ+b+c\right)+\left(37^\circ+c+d\right)+\left(\alpha+d+e\right)=180 ^\circ\times 5\\
\left(42^\circ+38^\circ+30^\circ+37^\circ\right)+\alpha+2(a+b+c+d+e)=180 ^\circ\times 5\\
147^\circ+\alpha+2\times 360^\circ=180 ^\circ\times 5\\
147^\circ+\alpha=180^\circ\\
\qquad \qquad \boxed{\alpha=33^\circ}.[/tex]

---

Solução elaborada pelos Moderadores do Blog.

Solução 2

---

Tomaremos por base a imagem que fizemos:

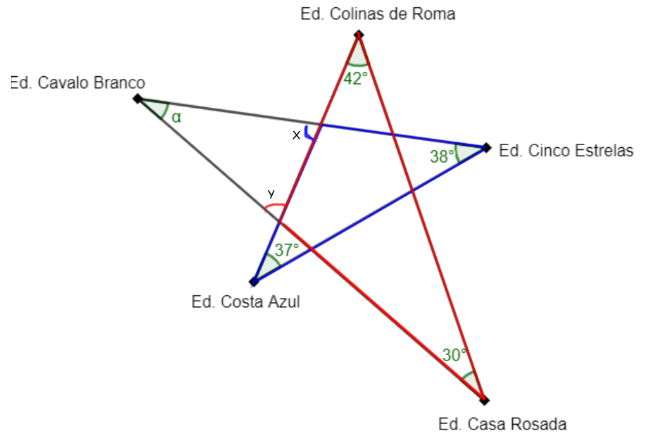
• No triângulo azul, observe que o ângulo de medida [tex]x[/tex] é um ângulo externo. Sabemos que a medida de um ângulo externo é igual à soma das medidas dos dois ângulos internos não adjacentes a ele; assim
  [tex]\qquad x = 37^\circ + 38^\circ \\
  \qquad x = 75^\circ.[/tex]
• Percebe-se, analogamente, no triângulo vermelho, que o ângulo cuja medida é [tex]y[/tex] é um ângulo externo. Daí:
  [tex]\qquad y = 30^\circ + 42^\circ \\
  \qquad y = 72^\circ.[/tex]
• Finalmente, observando o triângulo cujas medidas dos ângulos internos são [tex]\alpha[/tex], [tex]x [/tex] e [tex]y[/tex], como a soma das medidas dos ângulos internos é sempre [tex]180^\circ[/tex], teremos
  [tex]\quad \alpha+x+y = 180^\circ \\
  \quad \alpha+(x+y) = 180^\circ \\
  \quad \alpha + 147^\circ = 180^\circ \\
  \qquad \boxed{\alpha = 33^\circ}.[/tex]

---

Solução elaborada pelo COM Phidias.