Clique no botão abaixo para visualizar o problema.
Problema
Qual é a área de um triângulo que, em um plano cartesiano [tex]xOy[/tex], é definido pelos eixos [tex]Ox[/tex] e [tex]Oy[/tex] e pela reta cuja equação é [tex]2x+y+6=0\,?[/tex]
Solução 1
Inicialmente, vamos traçar o gráfico da reta definida por [tex]2x+y+6=0[/tex] em um plano cartesiano [tex]xOy[/tex].
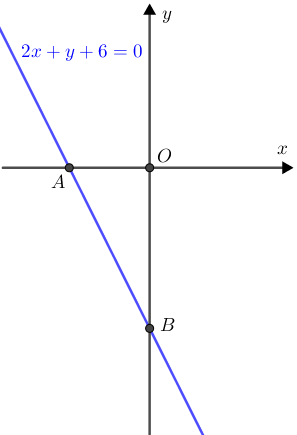
Observe que:
- fazendo [tex]x=0[/tex] na igualdade [tex]2x+y+6=0[/tex], obtemos que [tex]y=-6[/tex]
- fazendo [tex]y=0[/tex] na igualdade [tex]2x+y+6=0[/tex], obtemos que [tex]x=-3.[/tex]
Assim, as coordenadas dos pontos [tex]A[/tex] e [tex]B[/tex] são [tex]A=(-3,0)[/tex] e [tex]B=(0,-6)[/tex]. Com isso, o tal triângulo é um triângulo retângulo cujos catetos medem [tex]3~[/tex] e [tex]~6[/tex] unidades de comprimento.
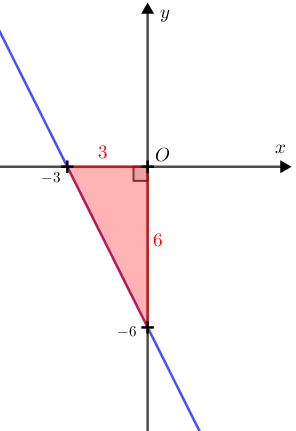
Dessa forma, a área do triângulo [tex]AOB[/tex] é dada por [tex]\dfrac{3 \times 6}{2}[/tex], ou seja, 9 unidades de área.
Solução elaborada pelos Moderadores do Blog.
Solução 2
Primeiramente, é preciso encontrar os três vértices do triângulo.
O primeiro é o ponto [tex](0,0)[/tex] e os outros dois são os pontos em que a reta [tex]2x+y+6=0[/tex] corta o eixo das Abscissas e o das Ordenadas.
Tomando [tex]x[/tex] como [tex]0[/tex] na equação [tex]2x+y+6=0[/tex], temos:
[tex]\qquad y + 6 = 0[/tex]
[tex]\qquad y = -6.[/tex]
Assim, a reta cruza o eixo das Ordenadas no ponto [tex](0,-6).[/tex]
Tomando [tex]y[/tex] como 0 na equação [tex]2x+y+6=0[/tex], temos:
[tex]\qquad 2x + 6 = 0\\
\qquad 2x = -6 \\
\qquad x = -3.[/tex]
Assim, a reta cruza o eixo das Abscissas no ponto [tex](-3,0).[/tex]
Colocando os três pontos em uma matriz quadrada de ordem 3 temos:
[tex]\qquad \begin{pmatrix} -3 & 0 & 0 \\ 0 & -6 & 0 \\ 1 & 1 & 1\end{pmatrix}[/tex]
O determinante dessa matriz é dado por:
[tex]\qquad \begin{vmatrix} -3 & 0 & 0 \\ 0 & -6 & 0 \\ 1 & 1 & 1\end{vmatrix}=18.[/tex]
Como a área de um triângulo é dada pela metade do determinante de sua matriz associada, temos que a área é [tex]\dfrac{18}{2}=9.[/tex]
Solução elaborada pelo COM Geomestres Slay.
Nível B – Questão Fácil
