Clique no botão abaixo para visualizar o problema.
Problema
Na figura, todos os triângulos são equiláteros e o segmento [tex]AB[/tex] mede [tex]15\text{ cm}.[/tex]
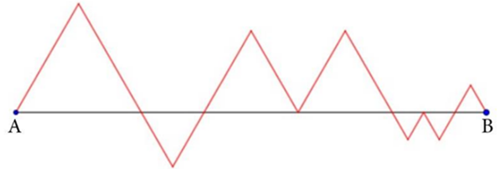
Calcule o comprimento, em centímetros, da linha vermelha.
Solução
Como os triângulos são equiláteros, vamos destacar os lados congruentes.
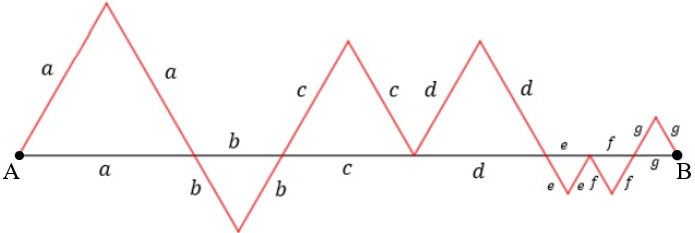
Observe que:
- o comprimento do segmento [tex]AB[/tex] é igual à soma [tex]a+b+c+d+e+f+g[/tex]
- o comprimento da linha vermelha é igual à [tex]2a+2b+2c+2d+2e+2f+2g.[/tex]
Do enunciado, podemos concluir que [tex]a+b+c+d+e+f+g=15\text{ cm}[/tex]; portanto, se denotarmos o comprimento da linha vermelha por [tex]\textcolor{red}{V}[/tex], segue que:
[tex]\qquad \textcolor{red}{V}=2a+2b+2c+2d+2e+2f+2g\\
\qquad \textcolor{red}{V}= 2\,\left(a+b+c+d+e+f+g\right)\\
\qquad \textcolor{red}{V}=2 \times 15=30.[/tex]
Assim, o comprimento da linha vermelha é [tex]30\text{ cm}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Participou da discussão o Clube Lapidando Vencedores Matemáticos.
Primeira Gincana de 2023 – Clubes de Matemática da OBMEP
Nível A – Questão Fácil
Nível A – Questão Fácil
