Clique no botão abaixo para visualizar o problema.
Problema
A figura abaixo mostra um mapa com 5 países.
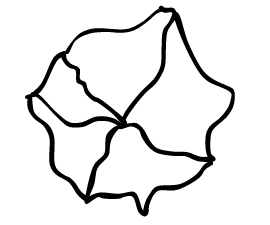
Qual é a menor quantidade de cores que permite colorir esse mapa, sendo que países com uma fronteira comum não podem ter a mesma cor?
Solução
Considere as regiões denotadas por A, B, C, D e E, como abaixo.
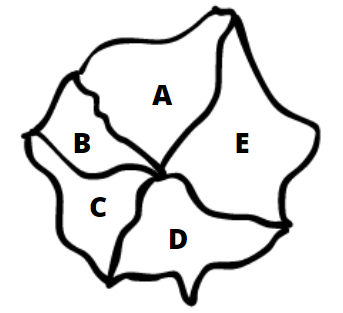
- Claramente não conseguimos colorir o mapa com apenas uma cor, pois países com uma fronteira comum não podem ter a mesma cor.
- Vamos, então, tentar utilizar apenas duas cores para colorir o mapa. Neste caso, a região A é colorida com uma cor, digamos, amarelo, enquanto E recebe outra cor, digamos, rosa. Como D é adjacente a E, D não pode ser colorida de rosa. Tentando usar apenas duas cores, colorimos D de amarelo. Raciocinando de maneira análoga, colorimos C de rosa.
Porém, chegamos a um impasse: B é adjacente a A, e não pode ser pintada de amarelo. Da mesma forma, B é adjacente a C, não podendo ser rosa.
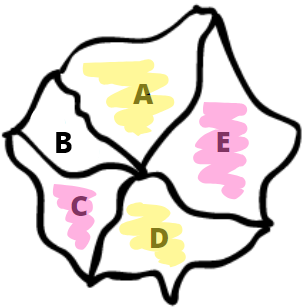
- Então, precisamos de uma terceira cor; digamos, azul.
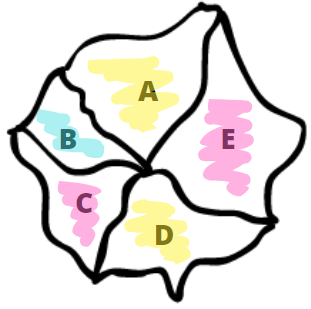
Assim, a menor quantidade de cores para colorir o mapa nas condições enunciadas é 3.
Solução elaborada pelos Moderadores do Blog.
Participou da discussão o Clube Lapidando Vencedores Matemáticos.
Primeira Gincana de 2023 – Clubes de Matemática da OBMEP
Nível A – Questão Fácil
Nível A – Questão Fácil
