✏ Link do problema para dispositivos da Apple.
Problema
Uma estudante de Matemática, na tentativa de encontrar a distância entre duas torres de altura [tex]2,5[/tex] metros, criou um modelo para o problema, utilizando um plano cartesiano [tex]xOy.[/tex]
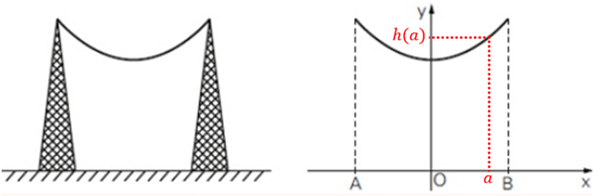
Na imagem da esquerda, podemos observar um fio preso nas extremidades das torres.
Na imagem da direita, vemos o modelo elaborado pela estudante.
Esse modelo supõe que o solo seja o eixo das abscissas, que os pontos A e B representam as bases das torres e que o ponto O, origem do plano cartesiano, é o ponto médio dessas bases.
A estudante estimou que a função [tex]h[/tex] que fornece a altura, em metros, correspondente a um ponto do fio que dista [tex]x[/tex] metros do eixo [tex]Oy[/tex] é descrita pela seguinte lei de formação [tex]\boxed{h(x) =2^{x}+\left(\dfrac{1}{2}\right)^{x}}.[/tex]
Diante do exposto, qual a distância, em metros, entre as bases das torres?
Solução 1
Seja [tex]x[/tex] a distância da base de uma das torres ao eixo [tex]Oy[/tex]. Assim, segue do enunciado que [tex]h(x)=2,5[/tex], ou seja,
[tex]\qquad \qquad 2^{x}+\left(\dfrac{1}{2}\right)^{x}=2,5.\qquad \textcolor{#800000}{(i)}[/tex]
Fazendo [tex]\boxed{2^x=t}[/tex] na igualdade [tex]\textcolor{#800000}{(i)}[/tex], temos:
[tex]\qquad t+\dfrac{1}{t}=\dfrac{5}{2}.[/tex]
e com isso, segue que:
[tex]\qquad 2t^{2}-5t+2=0.\qquad \textcolor{#800000}{(ii)}[/tex]
A equação [tex]\textcolor{#800000}{(ii)}[/tex] é uma equação do 2º grau; resolvendo essa equação, obtemos:
[tex]\qquad t=\dfrac{-b \pm \sqrt{\Delta}}{2a}=\dfrac{5 \pm \sqrt{9}}{4}=\dfrac{5 \pm 3}{4}[/tex],
ou seja, [tex] t=2\,[/tex] ou [tex]\, t=\dfrac{1}{2}.[/tex]
Como [tex]\boxed{2^x=t}[/tex], segue que:
[tex]\quad \textcolor{#800000}{(i)}\, 2^x=2 \\
\qquad x=1.[/tex]
[tex]\quad \textcolor{#800000}{(ii)}\, 2^x=\dfrac{1}{2} \\
\qquad x=-1.\\
~~[/tex]
Sendo [tex]x[/tex] uma distância, descartamos o valor negativo obtido e, portanto [tex]x=1.[/tex]
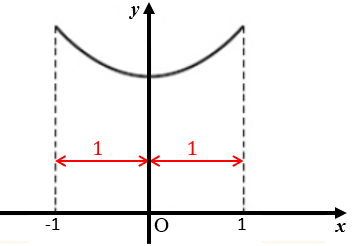
Mas, observe que a distância de um metro pode ser tomada à direita e à esquerda do eixo [tex]Oy[/tex]; assim, uma torre está com a base na posição [tex]~\left(-1,0\right)[/tex] e a outra com a base na posição [tex]~\left(1,0\right)[/tex] e, portanto, a distância entre elas é de [tex]2[/tex] metros.
Solução elaborada pelos Moderadores do Blog.
Solução 2
Como sabemos que ambas as torres possuem altura [tex]2,5m[/tex], podemos substituir esse valor para [tex]h(x)[/tex] na função dada, do seguinte modo:
[tex]\qquad \dfrac{5}{2}=2^x+ \left(\dfrac{1}{2}\right)^x.[/tex]
Escrevendo [tex]2^x=a[/tex], segue que:
[tex]\qquad \dfrac{5}{2}=a+\dfrac{1}{a}\\
\qquad \dfrac{5}{2}=\dfrac{a^2+1}{a}\\
\qquad 2,5a=a^2+1\\
\qquad 0=a^2-2,5a+1.\\
~~[/tex]
Pela fórmula de resolução de uma equação do 2º grau, temos:
[tex]\qquad \dfrac{-(-2,5) \pm \sqrt{(2,5)^2-4 \cdot 1 \cdot 1}}{2 \cdot 1}\\
\qquad \dfrac{2,5\pm\sqrt{2,25}}{2}\\
\qquad \dfrac{2,5 \pm 1,5}{2}\\
\qquad a_1=2 \text{ e }a_2=0,5.\\
~~[/tex]
Fazendo a substituição por [tex]2^x[/tex], temos:
[tex]\qquad (i)\, 2^x=2^1 \\
\qquad \quad x=1\\
\qquad (ii)\, 2^x=2^{-1} \\
\qquad \quad x=-1.\\
~~[/tex]
Como estamos trabalhando com medidas, o valor que procuramos para [tex]x[/tex] é positivo. Portanto, [tex]x=1[/tex] e, desse modo, sabemos que o ponto [tex]O[/tex] dista 1 metro da base de uma das torres.
Como [tex]O[/tex] é o ponto médio entre as duas torres, a distância entre as bases é, portanto, de 2 metros.
Solução elaborada pelo COM Geomestres Slay.
Nível B – Questão Difícil
