✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 9º ano do E. F.)
Em um grande loteamento há três terrenos retangulares vizinhos de dimensões [tex]a[/tex] por [tex]b[/tex], [tex]b[/tex] por [tex]c[/tex] e [tex]a[/tex] por [tex]c[/tex], sendo [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] medidas em metros. Esses terrenos possuem áreas de [tex]96\text{ m}^2[/tex], [tex]48\text{ m}^2[/tex] e [tex]72\text{ m}^2[/tex], respectivamente.
No mesmo loteamento, há outros três terrenos quadrados vizinhos de lados [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex].
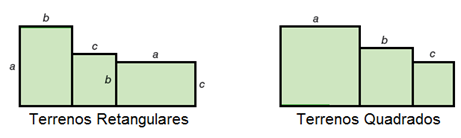
Qual a área total dos três terrenos quadrados?
Solução 1
A partir das informações dadas no texto, temos que:
[tex]\qquad a \cdot b=96; \qquad \textcolor{#800000}{(i)}[/tex]
[tex]\qquad b \cdot c=48; \qquad\textcolor{#800000}{(ii)}[/tex]
[tex]\qquad a \cdot c=72. \qquad\textcolor{#800000}{(iii)}[/tex]
Multiplicando as três equações, obtemos:
[tex]\qquad a^2 \cdot b^2 \cdot c^2=96 \cdot 48 \cdot 72\\
\qquad a \cdot b \cdot c=\sqrt{331\ 776^{~}}\\
\qquad a \cdot b \cdot c=576. \qquad\textcolor{#800000}{(iv)}[/tex]
Dividindo [tex]\textcolor{#800000}{(iv)}[/tex] por [tex]\textcolor{#800000}{(i)}[/tex], obtemos:
[tex]\qquad \dfrac{a \cdot b \cdot c}{a \cdot b}=\dfrac{576}{96}=6[/tex],
ou seja, [tex]\boxed{c=6 \text{ m}}.[/tex]
Dividindo [tex]\textcolor{#800000}{(iv)}[/tex] por [tex]\textcolor{#800000}{(ii)}[/tex], obtemos:
[tex]\qquad \dfrac{a \cdot b \cdot c}{b \cdot c}=\dfrac{576}{48}=12[/tex],
ou seja, [tex]\boxed{a=12 \text{ m}}.[/tex]
Dividindo [tex]\textcolor{#800000}{(iv)}[/tex] por [tex]\textcolor{#800000}{(iii)}[/tex], obtemos:
[tex]\qquad \dfrac{a \cdot b \cdot c}{a \cdot c}=\dfrac{576}{72}=8[/tex],
ou seja, [tex]\boxed{b=8 \text{ m}}.[/tex]
Finalmente, a área total dos três terrenos quadrados é
[tex]\qquad a^2+b^2+c^2=12^2+8^2+6^2= \fcolorbox{black}{#CAF3BA}{$244\text{m}^2$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
A partir das informações dadas, temos que [tex]~ab=96~[/tex], [tex]~bc=48~[/tex] e [tex]~ac=72~.[/tex]
Isolando [tex]a[/tex] na primeira e na terceira igualdades, segue que:
[tex]\qquad a=\dfrac{96}{b}~[/tex] e [tex]~a=\dfrac{72}{c}.[/tex]
Igualando os valores de [tex]a[/tex], temos que:
[tex]\qquad \dfrac{96}{b}=\dfrac{72}{c}\\
\qquad c=\dfrac{72b}{96}=\dfrac{3b}{4}.[/tex]
Isolando [tex]c[/tex] em [tex]bc=48[/tex], obtemos [tex]c=\dfrac{48}{b}.[/tex]
Igualando os valores encontrados de [tex]c[/tex] e observando que [tex]b \gt 0[/tex], temos que:
[tex]\qquad \dfrac{3b}{4}=\dfrac{48}{b}\\
\qquad 3b^2=192 \\
\qquad b=8.[/tex]
Descoberto o valor de [tex]b[/tex], podemos encontrar os outros dois valores:
|
[tex]ab=96 \\ 8a=96 \\ a=12.[/tex] |
[tex]\quad bc=48 \\ \quad 8 c=48 \\ \quad c=6.[/tex] |
Assim, se [tex]A[/tex] é a área total dos terrenos quadrados, segue que:
[tex]\qquad A=a^2+b^2+c^2\\
\qquad A=12^2+8^2+6^2\\
\qquad A=144+64+36\\
\qquad \fcolorbox{black}{#CAF3BA}{$A=244\text{ m}^2$}\,.[/tex]
Solução elaborada pelo COM União Fibonacci.
