Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir do 2º ano do E. M.)
Um cubo é seccionado nos pontos médios [tex]A, B[/tex] e [tex]C[/tex] de três arestas que concorrem em um vértice como mostrado na figura [tex]1[/tex].
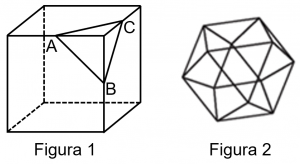
Tal procedimento é feito para todos os demais vértices do cubo e obtém-se, então, o sólido da figura [tex]2[/tex]: o Hexaedro (Cubo) Truncado. O novo sólido possui [tex]x[/tex] vértices, [tex]y[/tex] arestas e [tex]z[/tex] faces. Calcular [tex]x+y+z[/tex].

Lembretes e notações
Relação de Euler:
Seja [tex]V[/tex] o número de vértices, [tex]F[/tex] o número de faces e [tex]A[/tex] o número de arestas de um poliedro convexo. Então: [tex]V+F=A+2[/tex].
Solução
O hexaedro truncado possui [tex]6[/tex] faces quadradas e [tex]8[/tex] faces triangulares. Dessa forma, a quantidade total de faces é
[tex]\qquad F=z=6+8=14[/tex].
Por outro lado, cada aresta de cada face pertence a duas faces. Então, podemos escrever:
[tex]\qquad 6 \cdot 4+8 \cdot 3=2 \cdot A \\
\qquad A=24=y.[/tex]
Assim, pela Relação de Euler, temos:
[tex]\qquad V+F=A+2\\
\qquad V+14=24+2\\
\qquad V=x=12.[/tex]
Logo, [tex]x+y+z=12+24+14=50[/tex].
Solução elaborada pelos Moderadores do Blog.
Um applet para ilustrar
Você pode utilizar o applet abaixo para construir um hexaedro truncado e visualizar as suas 14 faces.
Além do cubo e do hexaedro truncado, você vai visualizar uma a uma as oito pirâmides que serão construídas e retiradas quando o cubo é seccionado nos pontos médios de três arestas que concorrem em um vértice. Para isso é só esperar o aplicativo carregar completamente e clicar sucessivamente nos quadradinhos que irão aparecer na janela da esquerda do aplicativo.
Instruções:
(1) Espere o applet carregar. (O aplicativo abrirá uma janela 3D; assim, ele pode demorar um pouquinho para carregar.)
(2) Para clicar nos quadradinhos, utilize o botão esquerdo do mouse.
(3) A qualquer momento do processo, você poderá movimentar o cubo que aparece logo no primeiro passo, assim como o poliedro final obtido. Para isso, clique em qualquer ponto da janela direita do aplicativo, mantenha o mouse pressionado e faça o movimento. (Se você estiver utilizando um celular ou um tablet, basta tocar levemente na janela do aplicativo e fazer o movimento.)
(4) Depois de construídas as oito pirâmides, ao clicar no último quadradinho que irá aparecer (Poliedro final obtido) o cubo inicial e todas as pirâmides serão retiradas para que você visualize o poliedro final.
(5) Para retornar à configuração inicial, clique nas setinhas circulares que aparecem ao lado da palavra Cubo.
OBMEP_ srdg, criado com o GeoGebra
