(A) Problemão: Ali Babão e a Trigésima Nona de suas Quarenta Equações

Problema
(Indicado a partir do 1º ano do E. M.)

Quantos números inteiros satisfazem a equação [tex]2^x \cdot (4-x)=2x+4[/tex]?

Solução

Vamos isolar o termo exponencial na equação dada:
[tex]\qquad 2^x \cdot (4-x)=2x+4 \\
\qquad 2^x=\dfrac{2x+4}{4-x}.[/tex]
Como [tex]2^x[/tex] é um número positivo, então [tex]\dfrac{2x+4}{4-x}[/tex] também deve ser positivo.
Então, vamos estudar o sinal dessa expressão; para isso, faremos isoladamente a análise de sinal das expressões [tex]2x+4[/tex] e [tex]4-x[/tex] e, a partir dessas análises, analisaremos o sinal da expressão [tex]\dfrac{2x+4}{4-x}[/tex] em função da variação de [tex]x.[/tex]
Vejamos.
[tex]\textcolor{#800000}{(1)}[/tex] Análises isoladas de sinal
Analisar o sinal de uma expressão significa saber para que valores de [tex]x[/tex] a expressão define um número positivo, um número negativo ou o número [tex]0[/tex]. E não precisa adivinhar, é só fazer continhas…

[tex]\textcolor{#800000}{(2)}[/tex] Análise de sinal da expressão [tex]\dfrac{2x+4}{4-x}.[/tex]
Vamos representar as análises de sinal do item anterior, considerando a reta real. Para isso, observamos que:

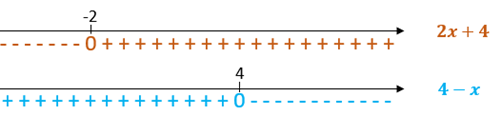
• a análise do sinal de [tex]2x+4[/tex] nos diz que à direita de [tex]-2[/tex] a expressão é positiva ; à esquerda de [tex]-2[/tex] a expressão é negativa e para [tex]x=-2[/tex] a expressão é zero.
• a análise do sinal de [tex]4-x[/tex] nos diz que à direita de [tex]4[/tex] a expressão é negativa; à esquerda de [tex]4[/tex] a expressão é positiva e para [tex]x=4[/tex] a expressão é zero.

Esquematicamente:

Lembrando das regrinhas de sinal para produtos e divisões:

• produto/quociente de números com sinais contrários é um número negativo;
• produto/quociente de números com mesmo sinal é um número positivo;

podemos, finalmente, obter a variação de sinal da expressão [tex]\dfrac{2x+4}{4-x}.[/tex]

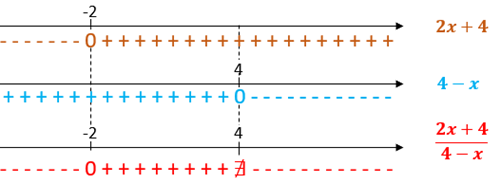
Concluímos, então, que para [tex]\dfrac{2x+4}{4-x}[/tex] ser positivo devemos ter [tex]-2 \lt x \lt 4[/tex], o que nos leva a concluir que [tex]x[/tex] só pode assumir esses valores: [tex]-1,\,0, \,1, \,2,\, 3[/tex].
Vamos, então, testá-los para verificar se eles satisfazem a igualdade [tex]~2^x=\dfrac{2x+4}{4-x}.[/tex]

• Para [tex]x=-1[/tex] temos:
  [tex]\quad 2^{-1}=\dfrac{2 \cdot (-1)+4}{4-(-1)} \\
  \quad\boxed{\dfrac{1}{2}}=\dfrac{-2+4}{4+1}=\boxed{\dfrac{2}{5}}[/tex]
  o que não é verdade;
• [tex]x=0[/tex]
  [tex]\quad 2^0=\dfrac{2 \cdot (0)+4}{4-(0)} \\
  \quad \boxed{1}=\dfrac{4}{4}=\boxed{1}[/tex]
  o que é verdade
• [tex]x=1[/tex]
  [tex]\quad 2^1=\dfrac{2 \cdot (1)+4}{4-1} \\
  \quad \boxed{2}=\dfrac{2+4}{3}=\boxed{\dfrac{6}{3}}[/tex]
  o que é verdade;
• [tex]x=2[/tex]
  [tex]\quad 2^2=\dfrac{2 \cdot (2)+4}{4-2} \\
  \quad \boxed{4}=\dfrac{4+4}{2}=\boxed{\dfrac{8}{2}}[/tex]
  o que é verdade;
• [tex]x=3[/tex]
  [tex]\quad 2^3=\dfrac{2 \cdot (3)+4}{4-3} \\
  \quad \boxed{8}=\dfrac{6+4}{1}=\boxed{\dfrac{10}{1}}[/tex]
  o que não é verdade.

Desta forma, os valores [tex]~\fcolorbox{black}{#eee0e5}{$0, 1, 2$}~ [/tex] são os únicos inteiros que satisfazem a equação dada.

Solução elaborada pelos Moderadores do Blog.