Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Fácil)
Sobre a face superior de um cubo de [tex]512 \, cm^3[/tex] de volume, é colocado outro cubo de [tex]8 \, cm^3[/tex] de volume de tal forma que os centros das faces de ambos coincidam.
Determinar a área total da superfície do sólido resultante da colagem, em [tex]cm^2.[/tex]
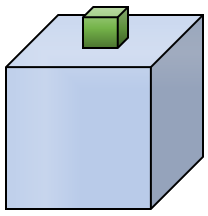
Solução
Como [tex]8^3=512 \, [/tex] e [tex] \, 2^3=8 \, [/tex], podemos concluir que o comprimento dos lados do cubo maior é [tex]8 \, cm \, [/tex] e o comprimento dos lados do cubo menor é [tex]2 \, cm.[/tex]
A próxima figura nos mostra os dois cubos; a região que aparece sombreada é a região comum aos dois cubos e, portanto, sua área deve ser retirada da área total de cada um dos dois cubos quando do cálculo da área total da superfície do sólido resultante da colagem.
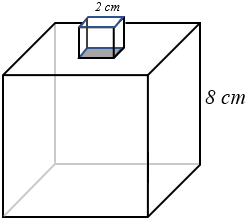
Assim, a área total solicitada é a soma das áreas totais dos dois cubos menos duas vezes a área sombreada, que nada mais é do que a área de uma das faces do cubo menor.
Como a área de cada face do cubo menor é [tex] \, 2^2=4 \, cm^2 \, [/tex] e a área de cada face do cubo maior é [tex] \, 8^2=64 \, cm^2 \, [/tex], a área [tex]A[/tex] solicitada no problema é dada por:
[tex] \qquad\boxed{ A=6\times 4+6 \times 64-2\times 4=24+384-8=400cm^2 }[/tex] .
Solução elaborada pelos Moderadores do Blog.
Nível C – Questão Mediana
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
