✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 1ª série do E. M.)
Duas velas do mesmo tamanho são acesas simultaneamente. A primeira dura [tex]4[/tex] horas e, a segunda, [tex]3[/tex] horas. Considere que cada uma das velas seja consumida a uma velocidade constante.
Em que instante, a partir das [tex]12[/tex] horas, as duas velas devem ser acesas de modo que, às [tex]16[/tex] horas, a altura de uma seja o dobro da altura da outra?
Adaptado de É divertido resolver problemas.
Solução 1
Imagine duas velas (azul e laranja) acesas, de mesmo tamanho, e tais que após um certo tempo a altura da vela azul seja o dobro da altura da laranja.
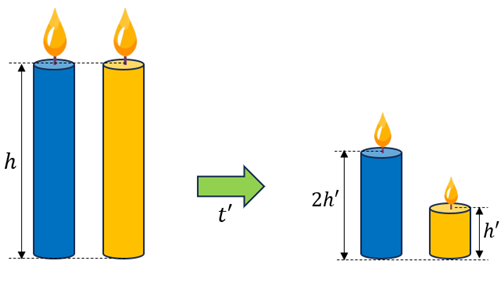
Como as velocidades de consumo são constantes, os gráficos das alturas em função do tempo são linhas retas. Assim, podemos esboçá-los da seguinte forma:
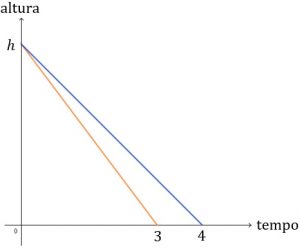
Vamos encontrar as equações das retas que estão representadas nos gráficos.
Como se tratam de retas, as alturas em função do tempo podem ser representadas por
[tex]\qquad \textcolor{blue}{A(t)_{azul}=a\cdot t +b}\qquad [/tex] e [tex]\qquad \textcolor{#FFA500}{A(t)_{laranja}=c\cdot t +d}[/tex],
sendo que a unidade de tempo é hora.
- No tempo [tex]t=0[/tex], temos [tex] \textcolor{blue}{A(0)_{azul}=b=h}~~[/tex] e, também, [tex]~~\textcolor{#FFA500}{A(0)_{laranja}=d=h}[/tex].
- No tempo [tex]t=4[/tex], temos [tex] \textcolor{blue}{A(4)_{azul}=4a+h=0}[/tex], donde [tex]a=-\dfrac{h}{4}.[/tex]
- Por outro lado, no tempo [tex]t=3[/tex] temos [tex]\textcolor{#FFA500}{A(3)_{laranja}=3c+h=0}[/tex], donde [tex]c=-\dfrac{h}{3}.[/tex]
Logo, as equações são:
[tex] \qquad \textcolor{blue}{A(t)_{azul}=\dfrac{-h}{4}\cdot t +h}~~[/tex] e [tex]~~\textcolor{#FFA500}{A(t)_{laranja}=\dfrac{-h}{3}\cdot t +h}[/tex]
No instante [tex]t'[/tex], temos:
[tex] \qquad \textcolor{blue}{A(t’)_{azul}=2h’}~~[/tex] e [tex]\textcolor{#FFA500}{A(t’)_{laranja}=h’}[/tex],
ou seja,
[tex]\qquad A(t’)_{azul}=2\cdot A(t’)_{laranja}[/tex].
Resolvendo a última equação encontrada:
[tex] \quad A(t’)_{azul}=2\cdot A(t’)_{laranja}\\
\qquad \dfrac{-h}{4}\cdot t’ +h = 2\cdot \left(\dfrac{-h}{3}\cdot t’ +h\right)\\
\qquad \dfrac{-t’}{4} +1 = \dfrac{-2t’}{3} +2\\
\qquad \dfrac{-t’}{4} +\dfrac{2t’}{3} = 2-1\\
\qquad \dfrac{5t’}{12} = 1\\
\qquad t’=\dfrac{12}{5}=2,4\text{ horas}=2\text{ horas e } 24 \text{ minutos}.[/tex]
Portanto, as velas precisam ser acesas às
[tex]\qquad 16-2,4=13,6[/tex] horas,
ou seja, às [tex] 13[/tex] horas e [tex]36[/tex] minutos.
Solução elaborada pelos Moderadores do Blog.
Solução 2
Suponhamos que as duas velas de mesmo tamanho sejam uma azul e outra alaranjada e que a vela azul dure [tex]4[/tex] horas e, a alaranjada, [tex]3[/tex] horas.
Antes de mais nada, observe que a vela azul demora mais para queimar totalmente; assim, é a vela azul que em um certo instante [tex]t[/tex] tem o dobro da altura da vela alaranjada.
Agora, vamos analisar as alturas das duas velas em dois momentos: no instante [tex]0[/tex] e no instante [tex]t[/tex].
- No instante [tex]0[/tex] as duas velas têm a mesma altura, digamos [tex]H[/tex] ([tex]H\ne 0[/tex]).
- No instante [tex]t[/tex], suponhamos que:
[tex]\quad \textcolor{blue}{H_1}[/tex] é a altura da vela azul;
[tex]\quad \textcolor{#FFA500}{H_2}[/tex] é a altura da vela alaranjada;
[tex]\quad H_1=2H_2[/tex];
[tex]\quad \textcolor{blue}{H=H_1+Q_1}[/tex];
[tex]\quad \textcolor{#FFA500}{H=H_2+Q_2}[/tex].
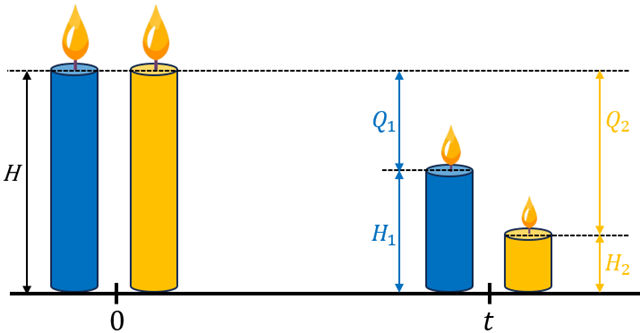
Como depois de acesas simultaneamente a vela azul queima em 4 horas e a alaranjada queima em 3 horas; podemos, a partir de duas regras de três simples, determinar quanto de cada vela queimou até o instante [tex]t[/tex], ou seja, em [tex]t[/tex] horas.
|
[tex]\begin{array}{c c c} \; H & \text{————–} & 4\text{ horas} \\ \; Q_1 & \text{————–} & t\text{ horas} \end{array}[/tex]
[tex]\quad \quad \textcolor{blue}{Q_1=\dfrac{ H \cdot t}{4}}[/tex]. |
[tex]\qquad \begin{array}{c c c} \; H & \text{————–} & 3\text{ horas} \\ \; Q_2 & \text{————–} & t\text{ horas} \end{array}[/tex]
[tex]\qquad \qquad \textcolor{#FFA500}{Q_2=\dfrac{ H \cdot t}{3}}[/tex]. |
Como [tex]~\textcolor{blue}{H_1=H-Q_1}~[/tex] e [tex]~\textcolor{#FFA500}{H_2=H-Q_2}[/tex], então [tex]~\textcolor{blue}{\boxed{H_1=H-\dfrac{ H \cdot t}{4}}}~[/tex] e [tex]~\textcolor{#FFA500}{\boxed{H_2=H-\dfrac{ H \cdot t}{3}}}[/tex].
Assim, de [tex]H_1=2H_2[/tex], segue que:
[tex]\qquad H_1=2H_2\\
\qquad H-\dfrac{ H \cdot t}{4}=2\left(H-\dfrac{ H \cdot t}{3}\right)\\
\qquad H\left(1-\dfrac{t}{4}\right)=2H\left(1-\dfrac{t}{3}\right)[/tex]
Como [tex]H \ne0[/tex], segue que:
[tex]\qquad 1-\dfrac{t}{4}=2\left(1-\dfrac{t}{3}\right)\\
\qquad 1-\dfrac{t}{4}=2-\dfrac{2t}{3}\\
\qquad \dfrac{2t}{3}-\dfrac{t}{4}=2-1\\
\qquad \dfrac{8t-3t}{12}=1\\
\qquad \dfrac{5t}{12}=1\\
\qquad t=\dfrac{12}{5}=2,4\text{ horas}=2\text{ horas e } 24 \text{ minutos}.[/tex]
Portanto, as velas precisam ser acesas às
[tex]\qquad 16-2,4=13,6[/tex] horas,
ou seja, às [tex]~\fcolorbox{black}{#eee0e5}{$ 13 \text{ horas e 36 minutos}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
