✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 1º ano do E. M.)
(Fuvest, 2011 – Adaptada) Na figura, o triângulo [tex]ABC[/tex] é equilátero de lado [tex]1[/tex], e [tex]ACDE[/tex], [tex]AFGB[/tex] e [tex]BHIC[/tex] são quadrados.
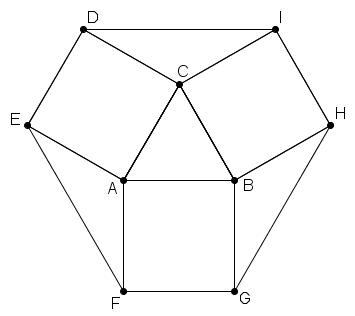
Quanto vale a área do polígono [tex]DEFGHI[/tex] ?

Lembrete
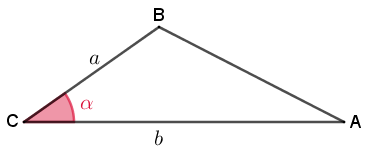
(1) Conhecidas as medidas [tex]a[/tex] e [tex]b[/tex] de dois lados de um triângulo [tex]ABC[/tex] qualquer e a medida [tex]\alpha[/tex] do ângulo compreendido entre estes lados, a área de [tex]ABC[/tex] é dada por
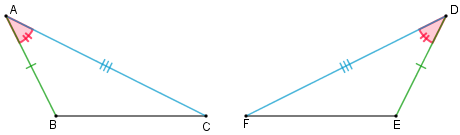
(2) Caso de congruência de triângulos L.A.L. (lado – ângulo – lado): Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes. (Para aprender mais, visite esta página.)
Solução
A maneira mais simples de resolver o problema é calcular a área dos sete polígonos em que o hexágono está decomposto e somar todas essas áreas.
- Como o triângulo [tex]ABC[/tex] é equilátero e tem lado medindo [tex]1[/tex], então a área deste é dada por
[tex]\qquad S(ABC) = \dfrac{1}{2}\times 1\times 1\times sen \; 60^{\circ} = \boxed{\dfrac{\sqrt{3}}{4}}[/tex]. - A área de um quadrado é dada pelo produto dos lados, então como a medida dos lados dos quadrados também são iguais a [tex]1[/tex], a área de cada um é dada por [tex]1\times 1[/tex], e portanto, os três quadrados somam área igual a [tex]\boxed{3}[/tex].
- Por fim, a área dos outros três triângulos pode ser calculada utilizando-se o Lembrete (1).
Perceba que os três triângulos são congruentes (Lembrete (2)); assim, basta calcularmos a área do triângulo [tex]AEF[/tex].
A medida do ângulo [tex]E\hat{A}F[/tex] é dada por [tex]360^\circ-90^\circ-90^\circ-60^\circ=120^\circ[/tex], como é possível observar na figura abaixo.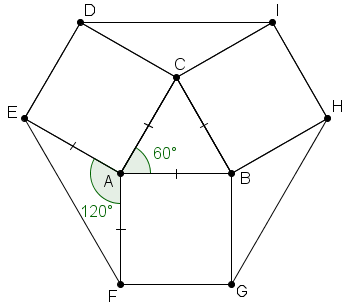
Assim, pelo Lembrete (1), a área do triângulo [tex]AEF[/tex] é igual a
[tex]\qquad \dfrac{1}{2}\times 1\times 1\times sen \; 120^{\circ} = \dfrac{1}{2}\times \dfrac{\sqrt{3}}{2} = \dfrac{\sqrt{3}}{4}[/tex];
portanto, a soma das áreas dos triângulos [tex]AEF[/tex], [tex]BGH[/tex] e [tex]CDI[/tex] é
[tex]\qquad 3\times \dfrac{\sqrt{3}}{4} = \boxed{\dfrac{3\sqrt{3}}{4}}[/tex].
Logo, a área do polígono [tex]DEFGHI [/tex] é
[tex]\qquad \dfrac{\sqrt{3}}{4}+3+\dfrac{3\sqrt{3}}{4} =~\fcolorbox{black}{#eee0e5}{$3+\sqrt{3}$}\,[/tex] unidades de área.
Solução elaborada pelos Moderadores do Blog.
