Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir do 1º ano do E. M.)
Uma fábrica de material de escritório está projetando um novo modelo de arquivo para guardar documentos.
O objeto será produzido a partir de uma placa retangular de dimensões [tex]50[/tex] cm e [tex]80[/tex] cm, na qual serão feitas duas dobras ao longo da maior dimensão da placa, como mostrado abaixo.
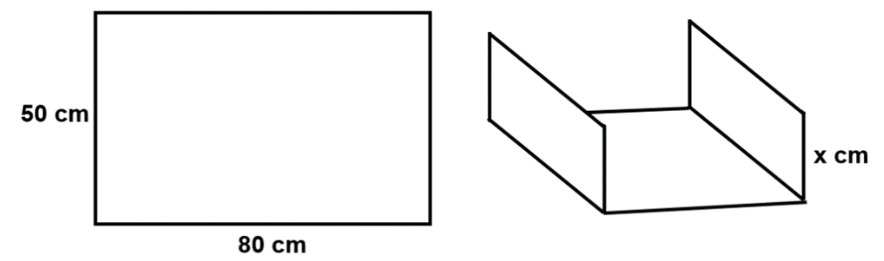
Qual deverá ser a medida da altura [tex]x[/tex] para que o arquivo formado tenha volume interno máximo?

Lembretes
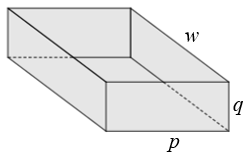
[tex]{\color{#800000}(1)}[/tex] O volume de um bloco retangular (ou paralelepípedo retorretângulo) cujos lados, expressos na mesma unidade de comprimento, medem [tex]p \, ; \, q \, ; \, w \, [/tex] é o produto dessas três medidas: [tex]\boxed{V=p \cdot q \cdot w} \, .[/tex]
[tex]{\color{#800000}(2)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,\, a\not=0[/tex], é uma parábola com eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
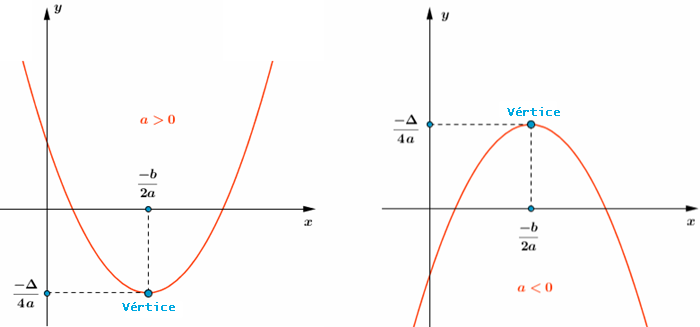
[tex]{\color{#800000}(3)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a}\, [/tex] e [tex]\, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(3)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução
Observe a figura
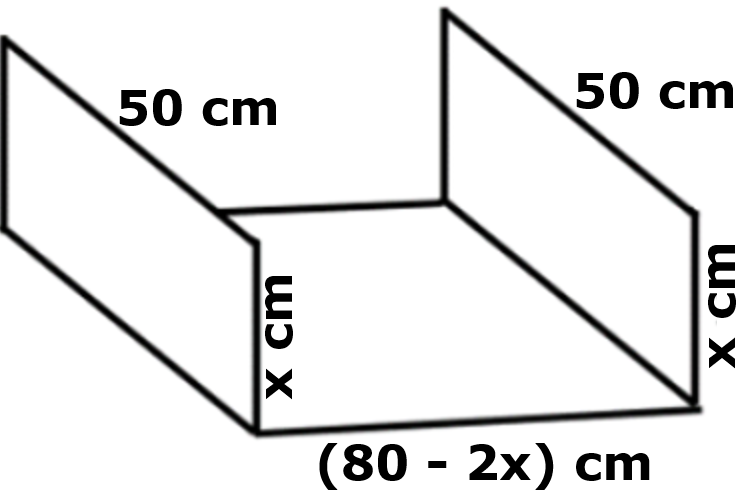
e perceba que o arquivo tem a forma de um paralelepípedo retorretângulo.
Portanto, o Lembrete (1) garante que o seu volume [tex]V[/tex] é dado por:
[tex]\qquad V=(80-2x) \cdot x \cdot 50[/tex]
[tex]\qquad \boxed{V=-100x^2+4\ 000x}\,.[/tex]
Assim, o volume do arquivo é dado por uma função quadrática definida por [tex]V(x)=-100x^2+4\ 000x[/tex], cujo gráfico é uma parábola com concavidade voltada para baixo, de acordo com o Lembrete (3) ([tex]a=-100[/tex]).
Neste caso, a medida da altura [tex]x[/tex] para que o arquivo formado tenha volume interno máximo é dada por
[tex]\qquad x_v=-\dfrac{4\ 000}{2 \cdot (-100)}=\,\fcolorbox{black}{#eee0e5}{$20 \text{ cm}$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
